【最新】公務員試験での数的処理おすすめ参考書、問題集ランキング

数的推理をしっかり得点源にしよう
数的処理が公務員試験の中で、苦手としている方が多い傾向にあります。今回は初級・中上級のレベルも合わせておすすめ公務員対策の数的処理の参考書・問題集テキストを紹介します。
畑中敦子の社会人採用決め手の数的処理
はじめに
本書は、公務員試験社会人(経験者)採用枠の受験生を対象に、教養試験(基礎能力試験)の最重要科目である数的処理の対策本として、おそらく初めて出版された書籍になります。

数的処理とは、判断推理(空間把握を含む)、数的推理、資料解釈を合わせた一般知能の非言語分野のことで、教養試験(基礎能力試験)のおよそ3分の1を占めます。
近年、公務員試験の社会人採用枠は拡大の方向にあり、経験の豊富な即戦力を積極的に採用しようとする傾向にあります。しかし、それに伴い、公務員への転職希望者も増えており、依然として狭き門です。その最初の関門が1次の筆記試験であり、重要科目である数的処理をしっかり対策することは、確実に土俵に上がるために必要なこととなります。
そこで、本書では、問題と解法のパターンが効率良く身につくよう、近年の主な社会人採用試験の過去問を徹底分析し、良問を厳選して分かりやすく解説するとともに、必要な公式やルールも余すことなく掲載しました。必ず、受験生の皆様のお役に立てると信じております。
皆様が合格、内定を勝ち取られ、国や自治体で新たなご活躍をされることを、心よりお祈り申し上げます。
2018年7月吉日
畑中敦子
目次
はじめに
目次
本書の使い方
プロローグ 試験情報と出題傾向
試験 File No.1 国家公務員
試験 File No.2 東京都職員キャリア活用
試験 File No.3 特別区職員経験者
試験 File No.4 地方公務員(県庁,市役所など)
第1部 判断推理
順序関係
位置関係
対応関係
リーグ戦
リーグ戦(応用)
トーナメント戦
数量条件からの推理
真偽
命題と論理
暗号
その他の推理
平面図形の構成
折り紙
一筆書き
移動と軌跡
軌跡の長さ
円の回転
立方体の展開図
正八面体の展開図
立体の切断
積み木
投影図
サイコロ
通過算と流水算
流水算
場合の数
確率
N進法
等差数列
数列
図形の計量
図形の面積
接線の性質と三平方の定理
直角三角形の3辺比
三平方の定理
直角三角形の角度
平行線と線分比
側面の最短経路
立体の体積
第3部 資料解釈
実数のデータ
割合のデータ
構成比のデータ
指数のデータ
増加率のデータ
本書の使い方

試験File No.1 国家公務員
#1 経験者採用試験(係長級)
民間企業等における実務経験のある人を、国の機関の係長級以上の官職に採用するための試験です。事務系(内閣府や各省庁の職員)のほか、外務省、国税庁、農林水産省などの省庁別に試験が実施されます。受験資格などは、試験により異なりますので、ホームページなどで確認して下さい。試験問題は、一般的な社会人対象の採用試験と比べるとレベルが高いので、しっかりとした対策が必要です。

#2 一般職試験(社会人(係員級)
国の機関の係員級の職員を採用するための試験です。2018年度の試験区分は技術や農業土木などで、地方整備局や防衛省の機関、全国の地方農政局、地方整備局での採用になります。2015~2018年度は、事務区分での試験がありません。
数的処理の出題傾向
例年、同日に実施される一般職(高卒)と同じ問題ですが、社会人採用試験の中では問題のレベルはやや高めです。
例年、判断推理7問(うち図形2問)、数的推理4問、資料解釈2問の計13問の出題です(次ページ参照)。
判断推理は、例年、最初に命題と論理が出題され、順序関係、位置関係、対応関係、数量条件からの推理などの問題が続きます。見た目にやや変わった印象を受ける問題もありますので、柔軟な視点で取り組む必要があります。図形分野では、展開図や積み木などの典型的な問題を始め、幅広い範囲から出題されており、やはり変わった問題も結構あります。
数的推理は、確率、比と割合、仕事算、図形(面積など)、速さの問題などが頻出で、多少の応用力を要する問題が多いです。
資料解釈は、図(グラフ)と表が1問ずつで、計算は余りありませんが、図表をきちんと読み取る力が必要となります。

#3 刑務官採用試験(社会人)
刑務所、少年刑務所、拘置所に勤務する職員を採用するための試験です。男女別、かつ地域別に区分があり、北海道、東北、関東甲信越静、東海北陸、近畿、中国、四国、九州に分かれています。2018年度の採用予定者数は、関東甲信越静が最も多く、男性20名、女性10名です。ほかはそれぞれ、若干名~10名の予定となっています。
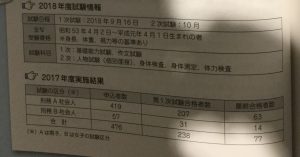
例年、一般職(社会人)と同様、判断推理7問(うち図形2問)、数的推理4問、資料解釈2問の出題で、傾向もやや似ていますが、レベルは一般職よりやや易しめです。
判断推理は、やはり、最初に命題と論理が出題され、他には、順序関係、位置関係が頻出ですが、割と幅広い範囲から出題されています。図形分野では、近年は、移動と軌跡、展開図が最頻出で、いずれも基本的な問題です。
数的推理は、場合の数、速さの問題、図形の面積、整数問題などが頻出で、基本的な問題が中心です。資料解釈は、図(グラフ)と表が1問ずつで、シンプルなデータが中心です。
過去3年間の出題内容
試験File No.2 東京都職員キャリア活用
専門的知識・スキル・経験へのニーズが高い分野ごとに区分を設定し、学歴区分に応じた職務経験のある人を採用します。合格者は主任級職として採用されますが職務経験や能力・専門性によっては、課長代理級での採用もあります。
 2017年度実施結果
2017年度実施結果
| 受験者数(人) | 合格者数(人) | |||
| 736(152) | 153(26) | |||
| (注)()内の数字は女性を内数で示す。 | ||||
例年、判断推理、数的推理、資料解釈、空間概念(判断推理の図形分野)が各4問という構成で出題されます(次ページ参照)。
判断推理(No.9~12)では、例年、No.9に集合算、No.11に確率と、4問のうち2問が実質的に数的推理の問題であることが多く、純粋な判断推理(図形除く)の問題は2問程度となります。集合算はやや面倒な問題もありますので、注意が必要ですが、確率は基本的な問題が多いです。判断推理では、順序関係の出題が多く、次いで、対応関係、位置関係などで、典型的な問題が中心ですがやや変わった! 題も時折あります。
数的推理(No.13~16) は、方程式の文章問題、速さの問題、整数などが頻山 最近は、数列もよく出題されています。4問のうち、図形が1~2問を占め、面積の問題が多く出題されています。いずれも難易度は標準的で、基本ができていれば解けるレベルです。
資料解釈(No.17~20) は、出題される図表のパターンが決まっています。過去問をしっかり研究して、図表の特徴を把握し、選択肢の内容についても、トレーニングしておくことをお勧めします。尚、過去3年分の試験問題は、東京都のホームページで公開されています。
空間概念 (No.21 ~24)は、例年、最後(No.24)に、移動と軌跡(図形の移動、軌跡の長さ、円の回転など)の問題が出題されています。その他では、図形の構成、展開図などが頻出で、やはり典型的な問題が中心ですが、面倒な問題も時折あります。

試験File No.3 特別区職員経験者
民間企業等で培った有用な経験を、即戦力として特別区政に生かすことを目的に実施されています。職務経験年数に応じて、主任での採用枠も設けられています。

数的処理については、経験者2級職、3級職とも同じ問題です。
東京都と同様に、例年、判断推理、数的推理、資料解釈、空間把握(判断推理の図形分野)が各4問という構成で出題されます(次ページ参照)。
判断推理(No.9~12)は、例年、No.9に試合(リーグ戦、トーナメント戦など、No.10に暗号の問題が出題されており、暗号は難問が多いので注意が必要です。その他には、マイナー分野を含む幅広い範囲から出題されていますが、近年は、関係、位置関係、対応関係などメジャー分野からの出題が中心で、いずれも基本な問題です。
数的推理(No.13~16)は、方程式などの文章問題、速さの問題、確率、数列などが頻出ですが、幅広い範囲からバランスよく出題されています。また、問題が例年1問出題され、相似、三平方の定理、日の問題など様々な問題か出されています。
資料解釈(No.17~20)は、例年、表と図(グラブ)が2問ずつ出題され、東京都と同様に、図表のパターンがある程度決まっています。過去3年分の話は、特別区のホームページで公開されていますので、過去問を研究しておいたほう
試験File No.4 地方公務員(県庁、市役所など)
近年、道府県庁、政令市のほとんどで民間経験者を対象とする社会人採用試験が行われ、全国の市町村役場でも、UIJターン希望者を歓迎し、公務員採用する傾向が高まっています。
採用試験は各自治体で行われ、6月下旬〜10月頃に1次試験を行う場合がほとんどです。
自治体によっては、主に民間企業で採用しているSPI3を実施するところや、教養試験を行わず作文や面接だけで採用するところもありますが、多くの場合、1次で教養試験が課せられます。
試験問題は自治体によってはオリジナルの問題を作成する場合もありますが、ほとんどは専門の公益法人が作成する問題を採用しています。問題にはいくつかの種類があり、どこの試験を採用するかは各自治体が決めますが、一般的な大卒者採用試験より難易度の低い問題を採用する場合が多いです。
ここでは、その中でも新しいタイプの試験である「社会基礎試験」と、以前から実施されている平均的なタイプの試験についてご紹介します。
#1 社会人基礎試験
2013年に登場した新しいタイプの試験で、これまでに多くの自治体や団体が採用しています。
試験は、「職務基礎力試験」と「職務適応性検査」から成り、一般的な教養試験に当たる「職務基礎力試験」は75問、90分、4肢択一で行われ、「社会的関心と理解を問う分野」「言語的な能力を問う分野」「倫理的な思考力を問う分野」の3分野で問題が構成されます。

数液処理は「倫理的な思考力を問う分野」として25問出題されており、内容は、判断推理、数的推理、資料解釈の一般的な問題ですが、難易度はかなり易しめです。
問題は易しいですが、1問当たり1~2分で処理する必要がありますので、早く正確に解く練習が必要です。
判断推理は、命題と論理、順序関係、位置関係、対応関係などが中心です。与えられる条件もわずかで、複雑な要素はほとんどありません。
数的推理は、速さの問題、仕事算、比と割合、確率など、頻出分野から出題が多 いですが、基礎学力を問うようなやや変わった問題も見られます。
資料解釈は、資料から選択肢の正誤を検討するという一般的な問題もありますが、資料から簡単な数値の計算をさせる問題も結構あります(本編の過去問参照)。
#2 県庁,市役所などの経験者採用試験
一般的な教養試験は、5肢択一で(50問, 150分) (40問, 120分) (30問, 90分)などの型があります。自治体や試験区分によっては、大卒採用と同じ試験問題の場合もありますが、ほとんどは、高卒採用と同じ問題や社会人向けの易しめの問題を採用しており、受験生の負担を軽減する方向にあります。

数的処理は、どの試験型でも教養試験のうちの約1/3を占め、10~16問程度の出題です。
判断推理は、5~8問程度で、そのうち2〜3問が図形の問題です。命題と論理、対応関係、順序関係、真偽、移動と軌跡、積み木などが頻出で、いずれも基本的な問題が中心です。
数的推理は、4~6問程度で、整数問題、速さの問題、図形(面積など)などの頻出分野からの出題も多いですが、マイナー分野も含め幅広い範囲から出題されています。
資料解釈は、1~2問で、実数や割合のデータが中心ですが、ややレベルの高い問題もありますので、時間配分に注意が必要です。
※道府県庁、市役所などの採用試験(社会人基礎試験を含む)の問題は、非公開(持ち帰り不可)となっています。本書に掲載されている過去問は、受験された方の情報を元に再現したもので、実際の試験問題とは一部異なる場合があります。
※試験情報は、2018年7月5日時点のものです。
文系女子のための数的推理 音声付きテキスト+トコトン問題集(公務員試験)
本書の特長
文系女子の公務員試験受験者のみなさんへ
本書は、公務員試験の数的推理科目の受験参考書です。数字や理系科目に弱いと自覚されている文系女子の方々のために
「算数・数学の基礎から復習できる」
「過去問の基本問題から標準問題を中心に掲載」
「基礎から段階的に学習できる」
「最新の出題傾向に準拠」
して、
できるだけやさしい解説で、途中で挫折することなく最終ページまで読め、短時間の学習時間で、確実に実力が付くようまとめられています。
本書の3大特典「音声講義」「問題集アプリ」「電子版」の入手方法等は、431ページをご参照ください。
本書は、数的推理対策用の教材です。著者、株式会社インプレスは、本書の使用による合格を保証するものではありません。
本書の内容については正確な記述につとめましたが、著者、株式会社インプレスは本音の内容に一切責任を負いかねますので、あらかじめご了承ください。
本書に掲載している会社名や製品名、サービス名は、各社の商標または登録商標です。
本文中に、TMおよびR、◎は明記していません。
インプレスの書籍ホームページ
書籍の新刊や正誤表など最新情報を随時更新しております。
http://book.impress.co.jp/
はじめに
この本を手にしていただき、ありがとうございます。
この本は、「数学がキライで数的推理の勉強が進まない…」という方のための公務員試験数的推理の入門書です。公務員試験の過去問を中心に、基本~標準問題を取りそろえています。

文系女子はもちろん、理系も体育系も芸術系も、男子学生もみんなウェルカムです。
数学が苦手でも大丈夫!
基本から着実に解いて土台作りをして、コツが掴めれば、数的推理に対する苦手意識がなくなること間違いなしです。
計算方法をすっかり忘れていても大丈夫!
数的推理に必要な「復習コーナー」を巻末に入れてあります。
「小数」「分数」から「方程式」まで、こっそりと復習しましょう。
この本が皆さんの公務員試験合格のお役に立てますように心から祈っています。
西川マキ
本書の特徴

第1章~第5章:本編
ウォーミングアップと練習問題にわかれています。
ウォーミングアップ
まずは肩慣らしです。例題と会話を楽しみながら、単元の雰囲気を味わってくださいね。

練習問題
解き方の確認をしたら、次は練習問題です。STEP 1から少しずつ難しくなりますが、解説も詳しく載っているから大丈夫!
第6章:実践問題
全て過去問からの出題です。
第7章:復習コーナー
計算や方程式など、数的推理に必要な内容が満載です。
もちろん詳しい解説付き!
本書の「過去問」
本書に載っている「過去問」は全て公表されている問題で、出典は略称で記載しています。
現在の略称に合わせているものもあります。
国家公務員I種→国家総合職、
国家公務員II種→国家一般職、
国家公務員Ⅲ種→国家一般職(高卒)
裁判所事務官1種・1種→裁判所総合職・一般職、
裁判所事務官II種→裁判所一般職(高卒)
記載がないものは本書のオリジナル問題です。
そもそも「数的推理」って?
ところで、「数的推理」は「割合」「速さ」「確率」「図形」などがあるみたいですが、「数的推理=数学」ですか?
確かに内容的には数学かもしれませんね。でも、数学と違って「丁寧な途中式」も「複雑な公式」も「図形の証明」も必要ありません。荒っぽい言い方をすれば、「5択の中から答えが見付かればよい」のです。
文系女子としては、図形の証明がないのはとってもハッピーなのですが、そんなに簡単に答えなんて出てきません…。
ところがどっこい! 解き方を身に付けてコツが掴めれば、簡単に答えが出るようになります。何度も同じ問題を解いて、解き方を覚えちゃいましょう♪
目次
はじめに
本書の特徴
そもそも「数的推理」って?
第1章 ペアで学習シリーズ
1-1 仕事算
「仕事」は全体の仕事量を勝手に決めておくとラク
1-2 ニュートン算
初めにある仕事+増えた仕事=全体の仕事量
1-3 順列&組合せ
PとCの使い分け、和の法則と積の法則がカギ
1-4 確率
「全部で何通り、そのうち何通り」を分数に
1-5 方程式&不等式
「方程式」は選択肢が問題を満たしているか計算もOK。
「不等式」は方程式で計算してもOK
第2章 割合シリーズ
2-1 割合
公式1つを覚えればすべて解決
2-2 比
4つのポイントを押さえればOK
2-3 濃度算
食塩水×濃度=塩をタテ・ヨコ・タテの順に表にしよう
2-4 損益算
店員の立場になって、原価、定価、売価、利益を書き出そう
第3章 速さシリーズ
3-1 速さ&流水算
または皮を使って、「流水算」は、速さを足したり引いたり
3-2 旅人算
2人まとめて「は×じ=き」
3-3 通過算&時計算
「通過」は距離に注目!「時計算」は距離の位に注目
第4章 整数シリーズ
4-1 約数&倍数
素因数分解、最大公約数、最小公倍数の計算の仕方をマスター
4-2 割り算の余り
いくつ少なければまたは多ければ、ぴったりかがポイント
4-3 規則性
規則が見付かれば計算で解ける
4-4 魔方陣&覆面算
「魔方陣」は真逆にある2数に注目
「覆面算」はこの数字しか入らないという所から
4-5 n進法
「△→10」は掛けていって、「10→△」は割っていって
第5章 平面図形シリーズ
5-1 長さ
三平方の定理と相似で、
5-2角度
三角形、平行線、円の性質を使いこなそう
5-3 面積
「三角形の面積」は面積比で勝負!
「見慣れない形の面積」は、図形を足したり引いたり移動したり
第6章 実践問題
基本-1
基本-2
応用-1
応用-2
第7章 復習コーナー
1-1 小数の計算
小数の足し算&引き算/小数の掛け算/小数の割り算
1-2 分数の計算
分数の足し算引き算/分数の掛け算/分数の割り算
1-3割合の単位
%と小数/歩合(0割0分)と小数/小数の割り算
1-4 距離・時間・速さの単位
2-1 最大公約数&最小公倍数
2-2 1次方程式&1次不等式
2-3 連立方程式
加減法/代入法
3-1 順列 (P)・組合せ (C)の計算
仕事算の解き方
ニュートン算の解き方
順列&組合せの解き方
確率の解き方
割合の解き方
比の解き方
濃度算の解き方
損益算の解き方
速さの解き方
流水算の解き方
旅人算の解き方通過算の
解き方
時計算の解き方
約数&倍数の解き方
「割り算の余り」の考え方
規則性の解き方
魔方陣(4×4)の考え方
覆面算の考え方
「長さ」の解き方
「角度」の解き方
「面積」の求め方
上・中級公務員標準数的推理―基礎から体系的に学べる“基本書”
はじめに
公務員試験の「数的推理」「判断推理」という科目を大学セミナーや種々の講習会で教えるようになって15年を超えた。講義で使用したプリント類の量 は、手元に残っているものだけでもかなりのものになる。これらをまとめたものが、本書の『標準 数的推理』であり、『標準 判断推理』であった。これ らの2冊に共通していえることは、体系的にまとめられ,応用範囲の広い考 え方を身につけることができるように書かれたものということである。「準備の段階で、過去の出題を調べ,分類するところから始めた。基本的な 概念を詳しく説明し、代表的な問題や応用範囲の広い問題を例題として解説し、少しずつ難易度の高い問題へ移るように配慮してある。枝葉末節と思われる問題はできる限り外し、思考力を伸ばすような問題を多く載せた。また今回の改訂にあたっては、例題や練習問題を大幅に増やした。

読者はまず、【基本事項】をじっくりと読み、用語や約束事、解答に至る考え方を身につけてほしい。【例題】は、読むだけでなく何度でも鉛筆を持って 実際に解答を追いかけてみるとよい。そして納得のいったところで【練習問 題]に進み、自分の理解したことを試してほしい。
「数的推理」は、「判断推理」と比較して,数学との類似性が高い分、読者 の読み方も多様になるであろう。文科系の学生諸君や、数学としばらく縁の なかった人たちは、何度も繰り返し【基本事項】や【例題】を読み、必ず鉛筆を手にして一つ一つ確認して進んでいくことをお勧めする。また,第4章 の剰余類の考え方は慣れるまでに時間がかかるので、後回しにして先に進んでもよい。
先の『標準 判断推理』がそうであったように、この『標準 数的推理』を 出版する目的の一つは、学生諸君がこれらの科目を学ぶときの「標準」的な道筋を指し示すことにある。本書および『標準 判断推理』がそうした要求を満たすものとなることを願っている。
2001年7月
田辺勉
目次
第1章 方程式
基本事項1 文字少使用,連立方程式解法
基本事項2 時計算
基本事項3 2次方程式
練習問題 練習問題の解説
第2章 不等式
基本事項1 不等式 基本事項22次不等式
練習問題 練習問題の解説
第3章 整数その1(倍数・約数)
基本事項1倍数・約数、倍数の見分け方
基本事項2 最大公約数・最小公倍数
練習問題
練習問題の解説
第4章 整数 02(剩余類)
基本事項1 剩余類 基本事項2 剩余類D演算
練習問題
練習問題の解説
第5章 整数 03(虫くい算·覆面算·魔方陣)
基本事項1 虫くい算、覆面算
基本事項2 魔方陣
練習問題 練習問題の解説
第6章 整数 その4 (n進法)
基本事項1 n進法
基本事項2 10進法の数をn進法に直す
基本事項3 n進法の数をm進方に直す
練習問題 練習問題の解説
第7章比・割合
基本事項1 比·割合
基本事項2 濃度
基本事項3仕事算
練習問題 練習問題の解説
第8章 速含·距離・時間
基本事項1 速さ・距離・時間
基本事項2 流水算
基本事項3 通過算
練習問題
練習問題の解説
第9章 座標・グラフ・数列
基本事項1 座標・グラフ
基本事項2ダイアグラム
基本事項3 数列
練習問題 練習問題の解説
第10章 平面図形その1
基本事項1 平行線
基本事項2 平行線と線分の比
基本事項3平面図形の面積
基本事項 4 線分比と面積比
練習問題の解説
第11章 平面図形その2(三平方の定理)
基本事項1三平方の定理
基本事項2 重心・外心・内心.
練習問題の解説
第12章平面図形その3(円)
基本事項1円周角の定理
基本事項2 接弦定理
基本事項3方べきの定理
練習問題
練習問題の解説
第13章 空間図形
基本事項1 基本的な空間図形
基本事項2体積・表面積
基本事項3面上の2点間の最短距離
練習問題
練習問題の解説
第14章 場合の数
基本事項1 場合の数
基本事項2 順列
基本事項3 組合せ
基本事項4 重複組合せ
練習問題 練習問題解説
第15章確率
基本事項1 確率
基本事項2 和事象·積事象
基本事項3独立試行の確率
練習問題
練習問題の解説
索引
第1章 方程式
周囲の空無を生み出し、しかもその空無を必要とする 白い光の球として星を見る、全く新しい奇妙な知覚。 ひいては、その知覚と関連して,私も全く同じように 暗黒の空無の中に吊り下げられているという感覚。私は星を見つめ、星は私を見つめていた。私と星との間 には釣り合いが保たれ、もしも意識を重量で現すことができるとすれば、正確に等しい二つの重さが天秤の水平状態を維持していた。
シージョン・ファウルズ『魔術師」
解說
この章では文字を使って、方程式を立てて解く問題を解説する。いわゆる文章題で、年齢算、時計算,過不足算のようなものも方程式でやさしく解いてみることにする。また2次方程式についても簡単に触れることにする。
基本事項1 文字の使用・連立方程式の解法
文字を使って数量を表したり、方程式を立てたりすることができる。以下の文音 から文字を用いて式を作ってみよう。
1辺がacmの正方形の周の長さは,4a(cm)
時速xkmでv 時間走ったときの距離 km は, z=xy と表せる。
十の位がx,一の位がりである整数は, 10x+y
120gのx%は,120× x /100=6 /5x(g)
半径rの球の表面積は47、体積は4/3πr
ここではまず、いくつかの代表的な2元連立1次方程式の解き方を具体例で示し、 方程式の解法の基本を習得してもらう。代入法や加減法などがあげられているが, いずれの場合も文字を減らしていき、よりやさしい方程式や、簡単な場合に還元し ていく。また、解が出たら面倒がらずにできる限り検算をする癖をつけてほしい。

②x=11 y=14
③x=5 y=ー1 /2
◆文章題への応用 文章題を方程式で解くには,普通,以下のような手順で行う。 文章で与えられた問題を熟読し、わかりにくけれは図や衣を使って意味をよく理 解し、与えられたものが何で,求めるものは何かをはっきりさせる。求めるもの。 あるいはそれに関連のある未知の数値を文字で表す。問題の数量関係を式で表す。 それを解いて、最終的に問題の要求している数値を出す。その解が問題に適してい
るかを確かめる。
過不足算,鶴亀算と呼ばれるなつかしい例でその様子を見てみよう。
(例)鉛筆を何人かの生徒に分けるのに、1人6本ずつ分けると2本不足し、1人5本ずつ分けると15本余る。生徒の人数と鉛筆の本数を求めよ。 (考え方) 求めるものは生徒の人数と鉛筆の本数の2つだが,文字(未知数)は少ないほうが楽なので、1つですめばそれにこしたことはない。生徒の 人数xがわかれば、鉛筆の本数は6x-2ですぐに求められるので1つだけにする。 (解) 生徒の人数をxとする。
「1人6本ずつ分けると2本不足する」ことから,鉛筆の本数は(6x-2)本 と表され、また,「1人5本ずつ分けると15本余る」ことから,(5x+15)本と も表される。したがって,この2つの式から次の方程式が得られる。
6x-2=5x+15 1 x=17
鉛筆の本数は、6x-2または5x+15にx=17を代入して求める。
6×17-2-31001
答生徒の人数17人 鉛筆の本数100本 (2) いかとたこ合わせて20匹いる。その足の数は、いかとたこを合わせて174本ある。いかとたこはそれぞれ何匹いるか。 (解) いかを匹,たこを匹と置く。
合わせて20匹だから x+y=320 足の本数を考えて10x+8y%3D174 これを解いて、
x=7,v=13 答いか たこ 135
【例題1-1】
父,母と子供が1人いる。母は父より4歳若く、父と母の年齢の和は子供の年齢の5倍に等しい。6年前には母の年齢が子供の年齢の3倍であったという。父と母の年齢の和が子供の年齢の4倍になるのは何年後か。
1 6年後
2 7年後
3 8年後
4 9年後
5 10年後
【例題1-1の解説】
基本事項2 時計算
時計の長針と短針が特別な位置関係になる時刻を問う問題。長針と短針が重なっ たり、一直線上に並んだり、直角になったりする時刻を求める。
12時の位置から時計回りに何度動いた位置に針があるかで考えるとよい。長針と 短針では一定の時間に動く角度に違いがあるので,単位時間あたりの動く量を求めておく。
1時と2時の間で長針と短針が重なるのは1時何分か。 (解)重なる時刻を1時x分とする。 「そのときの長針の位置は、0時(12時)から6x°のところ。 また、短針の位置は,0時から30~+0.5x°のところ。 長針と短針が重なるから。
6x=30+0.5x 両辺を2倍して、まとめると
11x=60
x=11/60=5+5/11
5 /11分は300/11秒=27+3/11秒
よって、求める時刻は約1時5分27秒
時計算
12時の位置から何度のところにあるか。
長針…1分あたり 6°
短針…1時間当たり 30°
1分あたり 0.5°
例題1−2
8時から1時間の間に、時計の長針と短針は1度だけ正反対の位置に一直線上に並ぶ。それは何時何分か。
1 8時9 1 /11分
2 8時10 9 /11分
3 8時10 10/11分
4 8時11 1/11分
5 8時11 11/9分
(例題1−2の解説)
求める時刻を8時x分とする。
長針の位置は、6x°
短針の位置は、8×30 +0.5x 長針の位置の180°反対側が短針の位置だから,
6x +180=240 +0.5x
両辺を2倍してまとめると、11x=120
x=11/120=10+11/10
よって、求める時刻は8時10 11/10分
基本事項 3 2次方程式
●因数分解
2次方程式の解法 (1)
解の公式
2次方程式の解法⑵

解と係数の関係
例題1−4
1辺が1cmの小立方体を組み合わせて立方体 A を作ると小立方体がx 個残る。 残った小立方体を立方体Aの表面に付着させてひと回り大きい(1辺の長さが1 cm 長い)立方体Bを作ると、今度は小立方体が75個残る。しかし,立方体B より さらにひと回り大きい立方体Cを作ろうとすると,小立方体が142個足りなくなる という。xはいくらか。
1 243
2 244
3 245
4 246
5 247
【例題1-4の解説】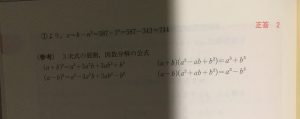
練習問題
No.1
ある試験で受験者の4割の人が合格したという。受験者全員の平均点は60 点で、合格者の平均点は合格最低点より15点高く,不合格者の平均点は合格最低 点より20点低かったという。合格最低点は何点か。
1 69点
2 68点
3 67点
4 66点
5 65点
No.2
A, B,C,Dの4人である品物を買った。 A は全体の代金の半分を, B は他の3人の出したお金の1/3を、Cは他の3人の出したお金の1/4を,Dは残りの 5500円を払った。この品物の代金はいくらか。
1 25000円
2 20000円
3 15000円
4 10000円
5 5000円
No.3
現在の父の年齢は子供の2.5倍である。8年後には、父の年齢が子供の年齢の2倍になるという。現在の父の年齢はいくつか。
1 30歳
2 35歳
3 40歳
4 45歳
5 50歳
No.4
みかん何個かを1人につき5個ずつ配ると10個余り、この人数の3倍より 5人少ない人数に、1人につき2個ずつ配ると8個不足する。このみかんを1人 につき6個ずつ配ると、何人に配ることができるか。
1 21人
2 22人
3 23人
4 24人
5 25人
No.5
午後6時から1時間の間に時計の長針と短針は1度だけ重なる。それは何時何分か。
1 午後6時32 6/11分
2 午後6時32 7/11 分
3 午後6時32分 8/11分
4 午後6時32分 9/11分
5 午後6時32分 10/11分
No. 6
現在2時で長針と短針のなす角度は60°である。長針と短針のなす角度が再び60°になるのは何分何秒後か。
1 20分27秒後
2 20分41秒後
3 21分16秒後
4 21分49秒後
5 22分10秒後
No. 7
A, B, C, D, Eの5人の月収の合計額は,130万円である。AとBの合計額は62万円、AとCの合計額は56万円,A とDの合計額は45万円, DとEのム 額は37万円である。Eの月収はいくらか。
1 12万円
2 14万円
3 17万円
4 20万円
5 22万円
No. 8
A, B2種類の茶があり,100gあたりの単価は A のほうがBより50円高い。また, A を100円分買ったときの量は、Bを100円分買ったときの量より10g 少ない。では、A, Bを合わせて600g買い、しかもAの量がBの量の2倍になるようにすると、購入金額はいくらになるか。
1 1250円
2 1300円
3 1350円
4 1400円
5 1450円
No. 9
No. 10
No. 11
両親と長女,次女の4人家族がいる。現在の両親の年齢の和は、2人の子供の年齢の和の5倍であるが、2年後には4倍になるという。また,現在の母親の年齢は、次女の7倍で,父親より4歳下であるという。長女と次女の年齢 いくらか。
1 2歳
2 3歳
3 4歳
4 5歳
5 6歳
No. 12
練習問題の解説
No. 1
受験者数を4人とすると、合格者数は0.4a 人,不合格者数は0.6a 人。受験 者の平均点が60点であるから、受験者の総得点は604点となる。求める合格最低点を差点とすると、合格者の平均点はx+15点,不合格者の平均点はx-20点。合格者の総得点は0.4a(x+15) 点,不合格者の総得点は0.6a(x-20) 点であるから、
60a=0.4a(x+15)+0.6a(x-20)
という方程式が得られる。
両辺に10をかけ、aで割ると、
600=4x+60+6x-120
10x=660
x=66
No.2
求める品物の代金をx円とする。また、B、Cの出した金額をそれぞれ b円、c円とすると,B,Cはそれぞれ、他の3人が出した金額の1/3、1/4を払ったから、
b=1/3(xーb) b=x /4
c=1/4(x -c) c=x /5
Aはx /2円払い、A、B、C、D4人の合計金額がxになるから、
x /2+x /4+x /5+500=x
両辺に20をかけて、分母を払うと、10x+5x+4x+10000=20x
x= 10000(円)
No. 3
現在の子供の年齢をxとすると,現在の父親の年齢は2.5x。8年後 年齢が子供の年齢の2倍になるから,
2.5x+8=2(x+8) . x=16
現在の父親の年齢は2.5x だから、2.5x=40
No.4
最初の人数をx人とする。みかんの個数は5x+10個。
この人数の3倍より5人少ない人数に、1人につき2個ずつ配ると8個不足するから。
5x+10=2(3x-5)-8
これを解いて、x=28
したがって、みかんの個数は150個。これを1人につき6個ずつ配ると,
150÷6=25
より、25人に配ることができる。
No.5
No.6
No.7
A, B,C,D,Eの5人のそれぞれの月収を a, b, c, d, e (万円)とす ると、
a+b+c+d+e=130…①
a+b=62 …②
a+c=56 …③
a+d=45…④
d+e=37 …⑤
②+⑤より a+b+d+e=99
①から引くと, c=31
③から、 a=25
④から、d=20
⑤から、e=17
よって、Eの月収は17万円。
No.8
No.9
No.10
解と係数の関係より,
a+β=4/3、aβ=-11/3
1/a-1+1/β-1=β-1+a-1/(a-1)(β-1)=a=β-2/aβ-(a+β)+1
=4/3-2/-11/3-4/3+1=4-6/-11-4+3=-2/-12=1/6
No.11
現在の次女の年齢をx歳とすると、母親は7x歳,父親は(7x+4)歳上
る。現在の長女の年歳をy歳とする。 現在の両親の年齢の和は、2人の子供の年齢の和の5倍であるから.
5(x+y)=327x+7x+4…….①
また、2年後に4倍になるから,
4{(x+2)+(y+2)}=7x+2+7x+6……. ②
②より, 14x=4(x+y)+8
これを①に代入して 5(x+y)=4(x+y)+8+4
x+y=12
これと①より, x=4, y=8
長女が8歳,次女が4歳なので、2人の年歳差は4歳。
No.12
Aの答は②を,Bの答は①を満たすはずだから、代入してみる。
61/26×8+27/13b=25 b=3
8/5a-61/5=-1 a-7
したがって,もとの方程式は
(7x+5y=-1
(8x-3y=25
これを解くと,(x,y)=(2,-3)
よって,x+y=2+(-3)=-1
数的推理がみるみるわかる! 解法の玉手箱 改訂第2版 (公務員試験)
算数・数学の世界で 「浦島太郎状態」なみなさんへ!
「判断推理・数的推理が教養試験突破のカギだ!」 判断推理・数的推理は公務員試験独特の科目ですし,大事な科目だということはわかっていても,「算数や数学なんて高校入試以来ちゃんとやってない」「数字が苦手だから文科系に進んだんだよ!」……という受験生にとっては、 どこから手をつけたらいいのかすらもわからない,やっかいな科目であることは事実です。

そんな、算数・数学から長い間遠ざかってしまって,今じゃ「√」だの 「π」だのいわれても,なんのこっちゃワカラナイ!という算数・数学の世界 の「浦島太郎状態」にある受験生のためにつくられたのが,この「解法の玉手箱」シリーズです。
本シリーズでは、数学浦島太郎状態の受験生でも実際の公務員試験に出題された過去問をなんとか解けるようにということで、過去問の解き方を手取り足取り詳しく解説しています。
まずは考え方の筋道を示して,計算式などもなるべく省略しないで記してありますし、問題を解いている中で疑問に思うようなことには、なるべく注をつけるようにしました。今までの問題集ではすぐギブアップしてしまったような受験生でも、算数・数学の「カン」を取り戻しつつ、判断推理・数的 推理をひととおり学べるようになっています。
「改訂第2版]では、最新問題を加えました。また,みなさんにもっとわかりやすいと感じてもらえるように、解説を検討,強化しました。
今まで判断推理・数的推理から逃げてきたみなさん! まずは本書をきっかけに、合格へ向けての準備を始めましょう!
資格試験研究会
本書の構成と使い方
●本書で取り扱う試験の名称表記について
本書に掲載した問題の末尾には,試験名の略称および出題年度を記載しています。
国家総合職:国家公務員採用総合職試験(平成23年度までは国家公務員採用I種試験)
国家一般職[大卒]:国家公務員採用一般職試験[大卒程度試験](平成23年度までは国家公務員採用II種試験
国家専門職「大卒]:国家公務員国税専門官採用試験,財務専門官採用試験 勞働基準監督官採用試驗,皇宮護衛官採用試驗大卒程度】,法務省專門職 員(人間科学)採用試驗,食品衛生監視員採用試驗,航空管制官採用試驗
裁判所:裁判所職員採用試験(総合職試験・一般職試験[大卒程度区分7)
地方上級:地方公務員採用上級試験(都道府県・政令指定都市・特別区。なお、東京都I類と特別区I類の問題はそれぞれ「東京都」「特別区」として います)
市役所:市職員採用上級試験(政令指定都市以外の市) 大卒警察官:大学卒業程度の警察官採用試験(なお、警視庁I類の問題は「警視庁」としています)
大卒消防官:大学卒業程度の消防官・消防士採用試験
●本書に収録されている「過去問」について
①試験実施団体により問題が公表されている試験については、公表された問題を掲載しています(平成9年度以降の国家公務員試験、平成13年度以降 の東京都,平成14年度以降の特別区,平成15年度以降の警視庁)。それ以 外の問題については、過去の公務員試験において実際に出題された問題を, 受験生から得た情報をもとに実務教育出版が独自に編集し、復元したものです。
②問題の論点を保ちつつ問い方を変えた、問題に不備があるところを補足したなどの理由で、実際に出題された問題に手を加えて掲載している場合が あります。
●本書の構成
実際の試験に何度も出ているような問題を選び,数学浦島太郎状態のみな さんが取り組みやすい内容,学習しやすい内容から順に、テーマ別に構成しました。
●例題
各テーマから最初に取り組みやすい問題・典型的な問題をピックアップし ました。まずはこの「例題」を解いてみて、感触をつかみましょう。
●練習問題
テーマをスムーズに理解できるよう、発展的な問題を選びました。解説は、 「例題」と同じように、詳しくていねいに記述してあります。全部解いて,実戦力をアップしましょう。
解説については、詳しくわかりやすいものにするため、解き方の手順を 「Beep」という形で示しています。また、ページの右側にある側注部分では、 竜宮城の仲間たちが次のような補足説明をしています。
問題を解くうえで重要な公式や考え方・知識など絶対に覚えておきたいところです。
難解なところの詳しい説明やフォロー、ちょっと発展的な内容などを紹介しています。
算数・数学が苦手な人のために、素朴な疑問に対する答えや、 基本的な知識のおさらいなどを載せています。
間違いやすいところや、引っかかりやすいポイント、注意点などについて説明しています。
実際の計算のしかたや筆算でのやり方を極力省略せずにていねいに記しています。
本文にある解き方とは別の解き方がある場合や、別の考え方などについて解説しています。
目次
第0章
数・数学のおさらい 足し算・引き算/かけ算・割り算/小数/分数/角度/面積/比/割合
第1章
数学苦手さんでもこれならわかる
1 角・面積の和の問題まとめてスッキリ解こう
2 面積の問題~パズル感覚で分割しよう
3 立体の問題 〜サクサクスライスして考えよう~
4 自然数の和の問題~やさしい公式をマスターしよう~
5 倍数・約数の問題 キーナンバーを見つけよう~
6 整数の問題~まず候補を見つけよう~
基本問題に取り組んでみよう(数式編)
7 方程式の問題をうまく決めれば解けたも同じ〜
8 不定方程式の問題条件を加えて答えを探そう~
9 不等式の問題~大小関係をつかめばOK~
10 順列・組合せの問題~「!」を使いこなそう~
11 確率の問題1 ~順列・組合せが大活躍~
12 確率の問題2 ~積の法則でもっと便利に~
第3章 基本問題に取り組んでみよう(図形編)
13 相似な三角形の問題~基本形をマスターしよう~
14 面積比の問題~面積の比こ辺の比~~
15 三平方の定理の問題~直角三角形を探せつくれ~
16 円の性質の問題~定理や公式を理解して納得~
17 円と接線の問題〜隠れた直角三角形はどこか~
第4章
図表でらくらくスピードアップ
18 ダイヤグラムの問題 ~相似を使ってゴールへ進め〜
19食塩水の問題 ~てんびんでカンタンに解ける!~
20 平均の問題~みんな同じと考えよう~
21 n進法の問題~まずは10進法に直すこと~
22 集合の問題 〜ベン図に数字を書いていく〜
第5章
得点アップ保証! 最強の解法はこれだ
23 速さの問題 〜比を使ってすばやく解く〜
24 流水算の問題 ~人の速さ、流れの速さ~
25 旅人算の問題~出会いと別れは速さの和と差~
26 仕事算の問題全体を1として割り振ろう~
27 ニュートン算の問題 ~「残高ゼロ」を式にしよう~
第6章
逆転の発想で正答が見える!!
28 ウラから攻める問題~ちょっと見方を変える~
29 余事象の確率の問題~引いた残りが求める答え~。
30最短距離の問題~直線をつなぎ合わせる~
31 選択肢を利用する問題倍数と分数に注目せよ~
第7章
最後はチカラワザで書き上げる
32覆面算・魔方陣の問題~隠された扉を開けるカギ~
33 数列の問題~見えない規則が見えてくる~
34書いて解く場合の数の問題~ひたすらすべてを書き出す~
35 書いて解く確率の問題~地道にもれなく根気よく~
36 いろいろな問題~手を動かせば糸口が見つかる〜
推理、数的推理と数的処理、課題処理、空間把握のカンケイ
試験によって呼び方に違いがあるので、ここで解説します。 公務員試験における教養試験(基礎能力試験)の一般知能系の問題 は、基本的には、
文章理解 …長文の読解力などを試す科目
判断推理・・・論理的思考力、推理力,判断力などを試す科目 一般知能」
数的推理・数量的な条件について考える力を試す科目
資料解釈・・・表やグラフを正確に読み取る力を試す科目
この4つに分けられます。
本シリーズは、このうちの判断推理と数的推理を取り上げているわけです。 では、数的処理,課題処理、空間把握ってなんでしょう? 数的処理は、判断推理と数的推理を合わせた総称として用いられる こともありますが、高卒程度試験や一部の地方自治体では数的推理と同じ意味で使われている場合もあります。
課題処理は、高卒程度試験において判断推理と同じ意味で使われています。
空間把握(空間概念)は、判断推理の中の図形問題(特に立体図形) をさしています。
また、判断推理と数的推理には明確な区分はありません。重複して いるテーマが存在しているほか、近年では判断推理と数的推理を融合 したような問題も多く見受けられます。 ・・・・とまあいろいろな呼び名があるわけですが、 総じて問われているのは、正答を導くための「推理 能力」と「情報の処理能力」です。これらは練習を積めば能力を上げることができますので、本書を使って、しっかりとトレーニングしていきましょう!
①足し算、引き算


②かけ算、割り算


③小数

④分数
⑤角度

⑥面積

⑦比

⑧割合
第1章 数学苦手さんでも これならわかる
1 角・面積の和の問題まとめてスッキリ解こう~
2 面積の問題 ~パズル感覚で分割しよう~
3 立体の問題 〜サクサクスライスして考えよう~
4 自然数の和の問題~やさしい公式をマスターしよう~
5 倍数・約数の問題 ~キーナンバーを見つけよう~
6 整数の問題~まず候補を見つけよう~
畑中敦子の数的推理ザ・ベストプラス【第2版】
はじめに
●数的推理とは
速さや確率の計算など、中学校の数学と算数をベースにした問題です。高校で習った公式も多少は必要になりますが、基本的なレベルです。
そして、数学と異なり、ときにはテクニックを使って解いたほうが早い問題もあります。

●なぜこのような科目が出題されるのか
割合や確率の計算など仕事に直結するものもありますが、まず、数字に対する感性が求められているといっていいでしょう。どのような仕事をするにも必要な ものですよね。
また、それ以上に求められているのは、思考力ではないかと思われます。そもそも、数学を勉強する目的は、論理的な思考力を養うことにあります。条件を分析し、論理的な筋道を立てて考え、結論へ導くという力です。
数的推理で試されているのも同じですが、数学と違って過程はあまり評価され ません。テクニックを使うなど柔軟な解法で、時間内で解決する事務処理能力が 求められていると思われます。
●どうやって勉強するのか
問題にも解法にもパターンがありますから、これをマスターして使いこなすことです。本番は時間との闘いですので、より早く正確に解く方法を身につけるこ とが大切です。
本書では、まず「PLAY!」でその項目の例題を取り上げます。解説を読んで解法 をマスターしてください。そのあと、「TRY!」で類題、「Challenge!」で応用問題 へと進んでいきます。すべての問題は、自力である程度の時間で解けるまで繰り返し解きましょう。
大切なのは、毎日コツコツと続けることです。時間を空けると鈍ってしまいますから、少しずつでいいので毎日勉強しましょう。
本書を手にした日から、1次試験の日まで、人によっては長い付き合いになる でしょう。良きパートナーとして皆さんの合格の一助を担えるなら、これほど嬉 しいことはありません。 皆さんの本試験でのご健闘と、合格、内定を心よりお祈りしております。
2018年2月吉日
田中敦子
目次
はじめに
INDEX
How to use The BEST
出題傾向
進捗状況チェック!
#1 約数と倍数は、整数の基本だよね?
#2 整数の問題は、数的推理の中枢だね☆
#3 整数解は、覚えてしまえばカンタンかも♪
#4 不等式なんて、大ざっぱでいいよね?
#5 比と割合は、センスが必要なの? 65
#6 利益算は、ホントに100円でいいの?
#7濃度は、どれもてんびんで解けるの?
#8 仕事算は、「全体を1」でOK?
#9 ニュートン算は、ワンパターンってホント?
#10 平均算は、合計に着目するの?
#11 年齢算は、whoとwhenが大事!?
#12 暦算は、昔の人の知恵袋だね♪ #13 覆面算は、どこから攻めるの?
#14 魔方陣は、コスパが高いってホント?
#15 集合算は、東京都のお気に入り?
#16 速さの問題、キライでしょ!?
#17 旅人算と通過算 どこがちがうの?
#18 流水算は、ちょっとちがうよね!? 173
#19時計算も、速さの問題なの?
#20 場合の数☆ まずは、数える問題か
#21 場合の数☆ 次は公式を使って
#22 最短経路は、たし算で解けるって!?
#23確率☆ やっぱり、出題率やっぱりNo.1!
#24 確率☆ 個性的な仲間たち
#25 2次関数って、数学だよね….?
#26 ORって、なに?
#27 剰余系と規則性解けると、気持ちイイ!
#28n進法は、システムを理解して!
#29 数列って、(シグマ)とか使うの?
#30三平方の定理 これって、何に使うの?
#31 相似って、何に使うの?
#32 円の定理なんて、覚えてないよね?
#33 立体図形も、平面で考えるんだね!?
#34 図形の変形って、パズルみたいだね☆
#35 角度の問題、これで最後だ!
How to use The BEST

出題傾向
主な試験の出題傾向と、頻出分野に対応する本書の項目の一覧だよ。 でも、数的推理の内容はすべてつながっている から、何を勉強しても力はつくんだ! だから、余り頻出度を気にしないで、すべての項 目を一通り勉強しよう! この資料は参考程度に活用してね!
国家公務員総合職・一般職・専門職
出題傾向
場合の数と確率が最頻出で、多いときは2~3問出題 されている。図形の計量も2問以上出題されることも あるが、近年はほぼ1問の出題で落ち着いている。その 他には、整数問題、比と割合、速さの出題が比較的多い が、広範囲に渡ってバランスよく出題されている。
特に頻出な項目 | #1 ~2, #5, # 16 ~ 18, #20~24, # 30 ~ 35 次に頻出な項目 | #3~4, #8 ~ 11, #15
裁判所職員総合職・一般職
出題傾向 場合の数と確率、図形の計量が最頻出だが、いずれも1問程度の年もあれば、3~4問出題される年もあり、安定しない。その他には、整数問題、比と割合、規則性を 発見する問題などがよく出題されている。以前は全件的にハイレベルであったが、近年は易化傾向にある。 特に頻出な項目 | #20~24, # 30 ~ 35
次に頻出な項目 | #1~2, #5~7, #16~18,#27~29
地方上級全国型・関東型・中部北陸型
出題傾向 整数問題と比と割合、及び、同系統の文章問題でほとんどを占める。図形の計量も例年1問の出題で安定して いる。全体的に個性的な問題が多く、一瞬戸惑うかも 知れないが、解いてみると易しい問題が多い。特に、近年は易化している。 特に頻出な項目 #1~7, #30~35 次に頻出な項目 #16~18, #20~24, #2327
東京都I類A・B
出題傾向 集合算と確率はほぼ毎年出題され、「新方式」や「技術」
では2問出ることもある。図形の計量も毎年1問の出題があるが、近年、「空間把握」分野でも計量問題が出 題されており、実質2問の出題となることが多い。その 他は広範囲から出題されており、マイナー分野からの 「出題も多い。数年前の過去問が繰り返し出題されてい
るので、過去問を数多く解いておく必要がある。 特に頻出な項目 #15, #23~24. #30~35 次に頻出な項目 #31~9, #13~14, #16~21,#327~29
特別区I類 出題傾向 近年、整数問題の出題が多く、2問以上出題されること
もある。その他では、速さ、場合の数と確率、比と割合 など、メジャー分野からの出題が中心である。図形の 計量は毎年1問だが、近年は、東京都と同様に、「空間把握」でも計量問題が出題されている。 特に頻出な項目 #31~2#16~18,#220~24, #330~35 次に頻出な項目[#5~7,#8~9, #27
※情報は2017年度試験終了時のものです。
約数と倍数は、頻出度 ★★★ 整数の基本だよね?
Yes! 約数や倍数は、整数を考える上で欠かせない要素!
この先もいろんなところでちょこちょこと顔を出してくるから、仲良くしておこう☆まずは中学校の復習から!
基本事項
①約数・倍数
整数A, B, Cにおいて、A=B×Cのとき、AをB, Cの倍数、B, CをAの約数と いいます。 たとえば、6=2×3ですから、6は2,3の倍数で、2,3は6の約数です。
②公約数・公倍数
いくつかの整数に共通する約数を「公約数」、共通する倍数を「公倍数」といい、 最も大きい公約数を「最大公約数」、最も小さい公倍数を「最小公倍数」といいます。そして、公約数は最大公約数の約数、公倍数は最小公倍数の倍数となります。
たとえば、12と18の最大公約数は6、最小公倍数は36なので、次のようになります。
12と18の公約数 ⇒ 最大公約数6の約数 = 1,2,3,6
12と18の公倍数 ⇒ 最小公倍数36の倍数 = 36,72,108
③最大公約数(G.C.M.)・最小公倍数(L.C.M.)の求め方
たとえば、「28,56,70」の場合、次の図のように並べ、共通の約数で順に割っていきます。3つ全部を割れる数がなくなったところで、そこまでの約数をかい 合わせ、最大公約数は2×7=14とわかります。
さらに、3つのうちの2つでも割れる数(図アの2と4)があれば続け、割れない数 (5)はそのまま下におろします。どの2つをとっても割れなくなった(「 互いに素」といいます)ところで、図のようにLの字にかけ合わせ、最小公倍数は2×7×2×1×2×5=280とわかります。

PLAY!1
A, B,Cの3人が、1月1日を初日として、Aは1日、Bは2日、Cは4日の間隔を あけて、夜9時から1時間の町内パトロールを実施した。1月2日以降、初めてこ の3人全員がそろって町内パトロールを実施した日までの間に、この3人がいず れも町内パトロールを実施しなかった日は何日あるか。
1. 2日
2. 5日
3. 8日
4. 11日
5. 14日
まず、各人がパトロールした日の規則性を確認しましょう。 Aは1日おきですから、初日から、その2日後、4日後、6日後…と2の倍数日後 にパトロールしたことになります。同様に、Bは3の倍数日後、Cは5の倍数日後 になりますので、3人全員がそろうのは、2.3.5の公倍数日給となりますね。
2, 3,5をともに割れる数はありませんので、最小公倍数は2×3×5=330ですから、1月1日から3人が初めてそろうのは、30日後の1月31日です。
そして、この30日間で、2,3,5のいずれかの倍数の日は、誰かがパトロール しているので、その日数を数えると、次のようになります。

Advice!
2, 3,5のいずれの倍数でもない数を直接数えると、「1, 7, 11, 13.12 23, 29」の8つなので、この程度なら直接数えたほうが早いね。でも、数が大きくなるとそうもいかないので、計算による解法も覚えておく必要があるんだ。 特に、ベン図の真ん中の数の足し引きでケアレスミスを起こしやすい。 この問題の選択肢は3日間隔だから、1日くらいの数えまちがいは命取りにはならないけど、選択肢が1日間隔とかの場合は慎重に数えようね。
TRY01
交通安全に関して企画した催しに、中学生, 高校生,大学生以上の3区分を設けて参加者を募集したところ、中学生54人, 高校生48人, 大学生以上90人の申し 込みがあった。その催しでは、中学生,高校生,大学生以上の3つの区分をそれぞ れ各チーム同じ人数になるような混成チームをできるだけ多く作って、チームご との得点を競わせることになっていた。ところが、ある1つの区分から12人の参 加取消があったため、実際にはチーム数を当初の予定より増やすことができた。
このとき、実際にできたチームの数はいくつか。
1.12
2.15
3.18
4.21
5.24
どのチームにも、中学生、高校生、大学生以上が、それぞれ同じ人数ずつになる ようにチームを作るわけですから、各区分の人数を各チームに同じ数ずつ振り分 けることになり、チーム数は各区分の人数の約数になります。 3区分それぞれの人数に共通する約数で、さらに、チームはできるだけ多く ることから、最大公約数を求めることになりますね。 まず、当初の予定について計算すると、図1のようになります。
公務員試験 新スーパー過去問ゼミ5 数的推理
刊行に当たって
公務員試験の過去問を使った定番問題集として、公務員受験生から圧倒的 な信頼を寄せられている「スー過去」シリーズ。その「スー過去」が、5回 目の大改訂を施して「新スーパー過去問ゼミ5」に生まれ変わりました。
「5」では,最新の出題傾向に沿うよう内容を見直すとともに,より使い やすくより効率的に学習を進められるよう、細部までブラッシュアップして います。

「新スーパー過去問ゼミ5」改訂のポイント
1 平成27~29年度の問題を増補
2 過去15年分の出題傾向を詳細に分析
3 1行解説・STEP解説,学習方法・掲載問題リストなど,学習効率向上のための手法を改良
4 本を開いたまま置いておける、柔軟で丈夫な製本方式を導入
もちろん,「スー過去」シリーズの特長は、そのまま受け継いでいます。
・テーマ別編集で、主要試験ごとの出題頻度を明示
・「必修問題」「実戦問題」のすべてにわかりやすい解説
・「POINT」で頻出事項の知識・論点を整理
本シリーズは、「地方上級」「国家一般職[大卒]」試験の攻略にスポット を当てた過去問ベストセレクションですが、「国家総合職」「国家専門職 [大卒]」「市役所上級」試験など、大学卒業程度の公務員採用試験に幅広く 対応できる内容になっています。
公務員試験は難関といわれていますが、良問の演習を繰り返すことで、合 格への道筋はおのずと開けてくるはずです。本書を開いた今この時から、日 標突破へ向けての着実な準備を始めてください。 あなたがこれからの公務を担う一員となれるよう、私たちも応援し続けます。
資格試験研究会
本書の構成と過去問について
●本書の構成
1 学習方法・問題リスト:巻頭には,本書を使った効率的な科目の攻略のしかたをアドバイスする「数的推理の学習方法」と,本書に収録した全過去問を一覧できる「 掲載問題リスト」を掲載している。過去問を選別して自分なりの学習計画を練ったり、学習の進捗状況を確認する際などに活用してほしい。
2 試験別出題傾向と対策:各章冒頭にある出題箇所表では,平成15年度以降の国家総 合職(国家I種)、国家一般職(国家II種),国家専門職(国税専門官),地方上級(全 国型・東京都・特別区) 市役所(C日程)の出題状況が一目でわかるようになっている。 具体的な出題傾向は、試験別に解説を付してある。
※市役所C日程については平成29年度の情報は反映されていない。
テーマ別出題頻度表示の見方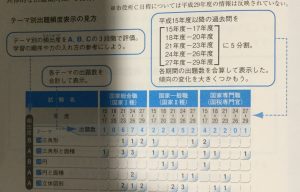
テーマ別の頻出度をA,B,Cの3段階で評価。 学習の順序や力の入れ方の参考にしよう。
平成15年度以降の過去問を
15年度-17年度
18年度-20年度
21年度-23年度
24年度-26年度
27年度-29年度
に5分割。
各期間の出題数を合算して表示した。 傾向の変化を大きくつかもう。
各テーマの出題数を 合計して表示。
3 必修問題:各テーマのトップを飾るにふさわしい、合格のためには必ずマスターしたい良問をピックアップ。解説は,各選択肢の正誤ポイントをズバリと示す「1行解説」, 解答のプロセスを示す「STEP解説」など、効率的に学習が進むように配慮した。また, 正答を導くための指針となるよう、問題文中に以下のポイントを示している
(アンダーライン部分):正誤判断の決め手となる記述
(色が敷いてある部分):覚えておきたいキーワード
「FOCUS」には、そのテーマで問われるポイントや注意点、補足説明などを掲載し ている。
必修問題のページ上部に掲載した「頻出度」は、各テーマをA,B,Cの3段階で評価し、さらに試験別の出題頻度を「★」の数で示している(★★★:最頻出,★★頻出,★:過去15年間 に出題実績あり、―:過去15年間に出題なし)。
4 POINT:これだけは覚えておきたい最重要知識を、図表などを駆使してコンパクトにまとめた。問題を解く前の知識整理に,試験直前の確認に活用してほしい。
5 実戦問題:各テーマの内容をスムーズに理解できるよう,バランスよく問題を選び, 詳しく解説している。問題ナンバー上部の「*」は,その問題の「難易度」を表してお り(***が最難),また,学習効果の高い重要な問題には⚡︎マークを付している。
必修問題と⚡︎マークのついた問題を解いていけば, スピーディーに本書をひととおりこなせるようになっている。
なお,収録問題数が多いテーマについては、「実戦問題1」「実戦問題2」のように問 題をレベル別またはジャンル別に分割し、解説を参照しやすくしている。
6 索引:巻末には、POINT等に掲載している重要語句を集めた用語索引がついている。 用語の意味や定義の確認、理解度のチェックなどに使ってほしい。
●本書で取り扱う試験の名称表記について
本書に掲載した問題の末尾には、試験名の略称および出題年度を記載している。
1 国家総合職,国家Ⅰ種:国家公務員採用総合職試験,国家公務員採用Ⅰ種試験(平成23年度まで)
2 国家一般職,国家Ⅱ種:国家公務員採用一般職試験[大卒程度試験],国家公務員採用Ⅱ種試験(平成23年度まで)
3 国家専門職,国税専門官:国家公務員採用専門職試験[大卒程度試験],国税専門官採用試験
4 地方上級:地方公務員採用上級試験(都道府県・政令指定都市)
(全国型):広く全国的に分布し、地方上級試験のベースとなっている出題型
(東京都):東京都職員I類B採用試験
(特別区):特別区(東京23区)職員Ⅰ類採用試験
※地方上級試験については、実務教育出版が独自に分析し、「全国型(全国型変形タイプ)」「関 東型(関東型変形タイプ)」「中部・北陸型」「法律・経済専門タイプ」「その他の出題タイプ」「独自の出題タイプ(東京都,特別区など)」の6つに大別している。
5 市役所:市役所職員採用上級試験(政令指定都市以外の市役所)
※市役所上級試験については、試験日程によって「A日程」「B日程」「C日程」の3つに大別している。
●本書に収録されている「過去問」について
1 平成9年度以降の国家公務員試験の問題は,人事院により公表された問題を掲載してい
る。地方上級の一部(東京都,特別区)も自治体により公表された問題を掲載している。 それ以外の問題は,受験生から得た情報をもとに実務教育出版が独自に編集し、復元し たものである。
2 問題の論点を保ちつつ問い方を変えた、年度の経過により変化した実状に適合させた。 などの理由で,問題を一部改題している場合がある。また,人事院などにより公表され た問題も,用字用語の統一を行っている。
CONTENT
公務員試験 新スーパー過去問ゼミ5
数的推理
「新スーパー過去問ゼミ5」刊行に当たって
本書の構成と過去問について
数的推理の学習方法
合格者に学ぶ「スー過去」活用術
学習する過去問の選び方
掲載問題リスト
第1章 数と式の計算
テーマ1 数の計算
テーマ2 素因数分解
テーマ3 約数・倍数
テーマ4 商と余り
テーマ5 記数法
テーマ6 数量問題
テーマ7 覆面算,魔方陣
テーマ8 数列
第2章 方程式と不等式
テーマ9 1次方程式
テーマ10 連立方程式
テーマ11 方程式の整数解
テーマ12 不等式
テーマ13 時計算,年齢算,平均
テーマ14 集合
テーマ15 速さ・距離・時間
テーマ16 旅人算,流水算
テーマ17 通過算
テーマ18 ダイヤグラム
テーマ19 比,割合
テーマ20 濃度
テーマ21 百分率,増加率
テーマ22 仕事算
テーマ23 ニュートン算
第3章 図形
テーマ24 三角形
テーマ25 三角形と面積
テーマ26 円
テーマ27 円と面積
テーマ28 立体図形
第4章 場合の数と確率
テーマ29 場合の数
テーマ30 順列
テーマ31 組合せ
テーマ32 確率(1)
テーマ33 確率(2)
テーマ34 確率(3)
索引
カバー・本文デザイン/小谷野まさを 書名ロゴ/早瀬芳文
数的推理の学習方法」
●過去問を解く重要性
次の2つの問題を見てほしい。
これは確率の問題であるが,酷似していることは明らかだろう。例題1は本書の旧版(『新スーパー過去問ゼミ4」)で、例題2は本書で取り上げた問題である。旧版で子 た読者は27年度の問題は難なく解けただろう(正答は例題1が1.例題2は2)。
このように、公務員試験の数的推理では、数年後に類似問題が出題されることが非常に多い。したがって、過去問に多く触れることが数的推理を制するための近道といっても過 言ではない。
そこで本書を利用するうえで効果的な学習方法・対策を示しておこう。
●効果的な学習方法・対策
数的推理は、一言でいうと「数学」である。「数学」といっても、そのほとんどの問題は、 中学卒業程度までの知識で解けてしまう。しかし、数学を苦手とする人には、少々やっかいなことに、文章題や図形、さらに確率といった分野が中心でとっつきにくい内容にな っている。それだけに、数学が得意な人と不得意な人とでは、教養試験(基礎能力試験) の中で得点差が出る科目である。
ここでは、数学があまり得意でない人向けの学習方法を伝授しよう。
1 重要ポイントの活用
本書では、各テーマに重要ポイントのコーナーがあり,このテーマの問題を解いていく うえで必要な数学の知識がまとめられている。ほとんどが、中学校の教科書程度の内容に なっているので、教科書がなくても学べるように構成されている。ここで,必要な公式や 基本事項を身につけてほしい。さらに,簡単な例題が添えられているので,これらを解く ことによって、基本問題を確実に解ける基礎・基本を学ぼう。
2 必修問題の解き方
必修問題には各テーマの典型的な問題を取り上げている。内容的には中程度の難易度の 「問題が多いので、初めて学習に取り組む際は解けなくてもかまわない。問題を解かずに読 み進めていくだけでもよい。その際、解法がSTEPごとに展開されているので,解法の流 れをつかんでほしい。
3 実戦問題の解き方
実戦問題は,原則として易しい問題から難しい問題の順に並んでいる。ここ数年の数的 推理の出題傾向は、数年前に比べると易しい問題が増えている。実は,難しい問題を取り こぼしても,それほど合否にはかかわらない。極端な話,五肢択一式なので20%は正解で きる。これをなんとか50~60%の正答率にもっていくには、基本から中程度の難易度の問 題を取りこぼさないような学習が大切である。この際、苦手な人は実戦問題の応用レベル は無視しよう。そのかわり、基本レベルに重点を置いて何度も繰り返し解くことをお勧め したい。特に、⚡︎の付いている問題は徹底的にマスターしよう。⚡︎と必修問題で約100問 あるので、最低限これらを身につけて、それを自信に試験に臨んでほしい。
4 学習のアドバイス
「幾何学に王道なし」 これは、紀元前の数学者であるユークリッドの言葉といわれている。ユークリッドは、 当時の国王の家庭教師として幾何学を教えていた。この王様は、向学心のある人だったが、 あまりにも幾何学(数学)が難しいため、ついに音を上げて、もっと幾何学を簡単に学ぶ 方法はないのかと尋ねたところ、それに答えたユークリッドの言葉が、この「幾何学に王 道なし」だったといわれている。国を支配する王様でも,数学はコツコツとやらなければ 身につかないという意味が込められている。皆さんも,数的推理の実力をつけるには、焦 らずにマイペースでコツコツと基礎づくりに励み、コツコツと応用力を身につけていこう。
◆お勧め学習方法
重要ポイントを読む→必修問題 を解く→実戦問題 を解く
基本レベルや⚡︎を中心に 繰り返し解く
合格者に学ぶ「スー過去」活用術
公務員受験生の定番問題集となっている「スー過去」シリースであるが,先輩たちは本 シリーズをどのように使って合格を勝ち得てきたのだろうか。弊社刊行の『公務員試験 受験ジャーナル』に寄せられた「合格体験記」などから,傾向を探ってみた。
自分なりの「戦略」を持って学習に取り組む!
テーマ1から順番に一つ一つじっくりと問題を解いて、わからないところを入念に調べ、納得してから次に進むという一見まっとうな学習方法は,時間をかけて学習を進 めている割には知識の定着がなかなか進まない。
やみくもに学習に取り組んで挫折している受験者をよそに,合格者はおおまかな学習計 画を立てて戦略を練っている。各章冒頭にある「試験別出題傾向と対策」を見て、自分が 受験する試験で各テーマがどの程度出題されているのかを把握し,「掲載問題リスト」を 利用するなどして、いつまでにどの程度まで学習を進めればよいか,学習の全体の流れを イメージしておきたい。
完璧をめざさない!ザックリ進めながら復習を繰り返えす!
本番の試験では、6~7割の問題に正答できれば、ボーダーラインを突破できる。裏を 返せば3~4割の問題は解けなくてもよいわけで、完璧をめざす必要はまったくない。学習する範囲を試験の頻出箇所に絞り、とにかくわからなくても先に進み、復習を繰り返す ことで力をつけていくというふうに意識改革を図ろう。
受験生の間では、「問題集を何周したか」がしばしば話題に上る。問題集は、1回で理解しようとじっくりと取り組むよりも、初めはさっくりと理解できた程度で先に進んでいき、 何回も繰り返し同じ問題集に取り組むことで徐々に理解を深めていくやり方のほうが、 学習効率は高い。合格者は「スー過去」を繰り返しやって、得点力を伸ばしている。
「スー過去」を自分に合わせてカスタマイズして使い倒す!
広い出発田の中から出のテーマ・過去問を選んでいる「スー過去」ではあるが、そ れでも430ページほどの分量がある。この分量をこなすのは無理だと敬遠している受験 生もいるようだが、実は合格者は「スー過去」を自分なりにアレンジして使っているので ある。必要な部分を自らピックアップして、学習ツールとして使い倒すことが、合格のカギといえる(次ページにカスタマイズの具体例を示したので参考にしてほしい)。
すぐに解説を読んでもOK!考えるのは時間のムダ!
合格者の声を聞くと「スー過去を参考書代わりに読み込んだ」というものが多く見受けられる。科目の攻略スピードを上げようと思ったら「ウンウン考えている時間」は一番のムダだ。過去問演習は、解けた解けなかったと一喜一変するのではなく、問題文と解説を 読みながら正解のポイントとなる知識を把握して記憶する反復演習なのである。
気になる知識は問題文に直接書き込んでいこう。どんどん知識を書き込んでいくと 「スー過去」自体が参考書化していくので、インプットの効率は格段に上がる。それを「 何周も回していくうちに、反射的に解答できるようになるはずだ。
学習する過去問の選び方
●具体的な「カスタマイズ」のやり方例
本書は全287問の過去問を収録している。分量が多すぎる!と思うかもしれないが、合 格者の多くは、過去問を上手に取捨選択して、自分に合った分量と範囲を決めて学習を進めよう。以下、お勧めの例をご紹介しよう。
1 必修問題と⚡︎のついた問題に優先的に取り組む!
当面取り組む過去間を、各テーマの「必修問題」と⚡︎マークのついている「実戦問題」 に絞ると、およそ全体の3割の分量となる。これにプラスして各テーマの「POINT」を チェックしていけば、この科目の典型問題と正誤判断の決め手となる知識の主だったとこ ろは押さえられる。
本試験まで時間がある人もそうでない人も、ここから取り組むのが定石である。まずは これで1周(問題集をひととおり最後までやり切ること)してみてほしい。
1を何周かしたら次のステップへ移ろう。
2 取り組む過去問の量を増やしていく
1で基本は押さえられても,1だけでは演習量が心もとないので、取り組む過去問の数 を増やしていく必要がある。増やし方としてはいくつかあるが、このあたりが一般的であ ろう。 ◎基本レベルの過去問を追加(難易度「*」の問題を追加)
◎受験する試験種の過去問を追加
◎頻出度Aのテーマの過去問を追加
これをひととおり終えたら、前回やったところを復習しつつ、まだ手をつけていない過 去問をさらに追加していくことでレベルアップを図っていく。
もちろん、あまり手を広げずに、ある程度のところで折り合いをつけて、その分復習に 時間を割く戦略もある。
●掲載問題リストを活用しよう!
「掲載問題リスト」では、本書に掲載された過去問を一覧表示している。 受験する試験や難易度・出題年度等を基準に、学習する過去問を選別する際の目安とし たり、チェックボックスを使って学習の進捗状況を確認したりできるようになっている。 効率よくスピーディーに学習を進めるためにも、積極的に利用してほしい。
実戦問題の中の 学資効率の高い問題にマークがついている。
難易度は、*易しい **やや難しい ***難しい
チェックボックスは、工夫次第でいろいろな情報を盛り込めるので、ぜひ活用してほしい。
掲載問題リスト




大卒程度 公務員試験 畑中敦子の数的推理の大革命! 令和版 (公務員試験/畑中敦子シリーズ)
はじめに
「こんな公式覚えて将来何の役に立つんだ!」って思いませんでしたか? 中学、高校で数学の勉強しているときです。特に、数学嫌いのアナ・タ!
確かに、数学で習った公式や定理を生かせる仕事に就く人は一握りでしょうね。でも、 数学を勉強する理由は、そこじゃあないんです。「論理的な考察力を養う」ことが本来の目的なんですね。与えられた条件と、公式などの情報から、論理的に正解を導く練習をする。それは社会に出てからのあらゆる問題を解決する能力を養うことに繋がるんですね。

そして、数的推理ですが、これは数学とはちょっと違います。数学は正解を導く過程 が重視されますが、数的推理は答えが合っていればそれでいい! 要するに、解決でき ればいいんです。ちょっと実践的な感じでしょうか。でも、これはこれで、やはり、「論 理的な考察力」と「事務処理能力」が求められるわけなんですね。
本書は、数学を学ぶのとはちょっと違った目線というか、「正解を出す」ことに拘っ た解説していますので、数学が得意な方には違和感を持たれる部分もあるかもしれませ ん。でも、これは数的推理なので、そういう解き方もあるんだ、くらいで見てください。
最近では、文系、理系を問わず、数学を学ぶことの大切さが見直されています。「数 字に弱いんで…」じゃ済まされない時代になろうとしているわけです。新しい時代の肥 を取る皆さんには、合格のためだけではなく、仕事のできる公務員になって頂くために も、是非、数的推理を得意科目にして頂きたいと心から思います。
本書を活用下さった皆さんが、合格、内定を勝ち取られますよう、心から応援してお ります。
平成31年4月
畑中敦子
CONTENTS
■はじめに
■本書の効果的活用法
■ 側注表記の意味
SECTION01 約数・倍数の驚くべき価値!
SECTION02 比·割合のスゴイ性質!
SECTION03 たかが整数とあなどるなかれ!
SECTION04 覆面算は大胆に!
SECTION05 魔方陣も大胆に!
SECTION06 集合!ほぼベン図でイケる!
SECTION07 仕事算は基準を選べ!
SECTION08 ニュートン算はワンパターン
SECTION09 食塩水はてんびんで!
SECTION10 利益算は100円でOK!
SECTION11 平均算は合計にもどして!
SECTION12 年齢算!現在・過去・未来!
SECTION13 不等式!その範囲の整数ってコト!
SECTION14 余り!その意外な規則性!
SECTION15 n進法は10進法に直して!
SECTION16 数列!公式は無理して使うな!
SECTION17 最大値・最小値!1番じゃなきゃ!
SECTION18 その他いろいろな文章題!
SECTION19 は・じ・きの公式は奥が深い!
SECTION20 旅人算と通過算はセットで!
SECTION21 流水算と時計算はそれぞれの個性で!
SECTION22 場合の数!足すことと掛けること!
SECTION23 場合の数のいろいろな問題
SECTION24 確率も足すことと掛けること!
SECTION25 確率の個性的な問題
SECTION26 図形の計量の主役たち!
SECTION27 三角形のいろいろな性質
SECTION28 図形の計量のいろいろな問題
SECTION29 円の定理は角度の定理
SECTION30 立体図形は次元を落とせ!
付録
公式集
法則集
定理集
一問一答
本書の効果的活用法

SECTION
数的推理を 30 のセクショ ンに分けたよ。それぞれ 個性があるけど、苦手分 野を作らないようにね!
タイトル
赤い文字が、このセ クションの項目だか らね。
重要度
満点は★5つ。頻出度 が高い項目はもちろん、 頻出度が低くても大事 な項目は★が多い。
ガイダンス
予備校の講義で初め に話すようなイント ロダクション。ここ で、気を引き締めた り、リラックスした り
パターン
まずは、典型的なパ ターン問題から始め よう! この問題を 通して解法パターン を覚えるんだ。
出典
最新の本試験問題を中心に、古き良き問題 も豊富に掲載。出典がないのは、過去問を ベースに先生が作った問題だよ。7ページ の「出典表記の補足」も参考にしてね。
Exercise
パターン問題が解け たら、ここで力試し! まずは自力で解いて みよう!
側注
必要な公式や法則、そ してボクのアドバイス など、本文の先生の解 説をさりげなくサポー トするよ。それぞれの 内容は次ページ!
側注表記の意味
ワンポイントアドバイス One Point Advice
多くの条件に登場する(情報が 豊富)ものに注目することが、 解法の第1歩!
失敗しないためのアドバイス! ここは欠かさず読んでね!
ちょっと補足
2倍して、一の位が0,2,4 になるのは、0,1,2,5,6, フがあるけど、偶数は0と2と 6だけだね。
先生の解説にちょい足し☆ けっこう役に立つと思うよ!
ナットクいかない方はこちら
3種類を1枚以上で計15枚買 うんだから、1種類は Maxo で13枚でしょ!?
「!?」って思ったら読んでね。 思わなかったら飛ばしてOK!
計算しよう!
外項の積=内項の積より、
2(7a + x) = 3(4a + x)
14a + 2x = 12a + 30
x=2a
方程式などの計算はここで確認。 必ず自分で計算してから、答え合 わせに使ってね!
ここがポイント!
文字通り、その 問題のポイント! 大事なところだ からしっかり理 解してね!
裏ワザ!
そんな大げさなも のじゃあないけど、 ちょっと裏ワザっ ぽいところにこの マーク!
公式5
1 距離=速さ×時間
2 速さ=距離÷時間
3 時間=距離÷速さ
法則3
指数法則
1 am×an=am+n
2 (am)n=amn
定理8
底辺分割の定理
図において、2つの三角形 の面積をS, S2とすると、
S1: S2=p:q
覚えておくと便利!
問題を解くのに必要な公式などで、巻末の付録 にもまとめてあるよ。それぞれに対する「一問 一答」もあるから、練習に使ってね!
本書に掲載している過去問の出典表記の補足です
| 国家一般職 | 国家一般職(大卒)の問題です |
| 国家Ⅰ種 | 現在の「国家総合職」にあたる試験です(2012年より改定) |
| 国家Ⅱ種 | 現在の「国家一般職(大卒)」にあたる試験です(2012年より改定) |
| 国税専門官 | 2012年の改定以降は「国家専門職」と表記しています |
| 裁判所事務官 | 2012年の改定以降は「裁判所職員」と表記しています |
| 東京都Ⅰ類 | 2008年の改定以降は、A(院卒)、B(大卒)に分類されています |
| 地方上級 | 主にA日程の再現問題です※ |
| 市役所 | 主にB、C日程の大卒採用試験の再現問題です※ |
※地方上級及び市役所の試験問題は非公開です。本書に掲載されている問題は、LECが受験生の情報をも とに再現したもので、実際の開額とは内容、表記が異なる場合があります。
公務員試験「数的推理」が面白いほどわかる本
はじめに
●インプット→アウトプットの正しい勉強を
「最強のインプット本を作りたい」
講師として書籍・教材を執筆するなかで、このような想いを持っていました。

公務員試験は、大学入試のように少ない科目を深く掘り下げるのではなく、多くの科目の浅い知識を問うてきます。科目数が多く、どこまで知識を学べばいいかわからないので、公務員試験は知識を習得(インプット)してから問題を解く(アウトプット)という勉強がしにくい試験だといわれています。そのため、独学で公務員試験の対策をする受験生の多くは,問題を解きながら知識を覚えるのが現状です。しかし、その勉強法は、スポーツで例えると,練習をまったくしないで練習試合に出続け、試合の中で上達していかなくてはならないようなものです。いかに非効率な勉強法か、おわかりいただけると思います。公務員試験を突破するためには、「正しい勉強法」が必要です。
●「数的処理」とは?
「数的推理」「判断推理」「図形」「資料解釈」の4つを合わせて、「数的処理」とよびます。本書『公務員試験「数的推理」が面白いほどわかる本』と、姉妹本である『公務員試験「判断推理」が面白いほどわかる本』では、特に重要な数的推理・判断推理・図形を扱います。
数的処理は教養試験の約40%を占める重要な科目です。しかしながら、アウトプットから学習を始めるせいで、いくらやっても数的処理が得意にならない受験生を何人も見てきました。
「せめて数的処理だけでも,しっかりとした知識を提供できる教材があるべきだ。」「じゃあ俺が作る!!」
という思いで本書を書き上げました。史上最強の「参考書」だと胸を張っていえます。
●本書で身につけられること
数的処理の問題は次の2つに大別できます。
①知識を要し,過去にも出題されたことがある有名な典型問題
②知識は必要としないが、ひらめきだけで解く非典型的な問題
本書は①を主なターゲットにし、頻出問題を解くために必要な知識をわかりやすく解説しています。すべての問題が次の試験に出てもおかしくない、合格に必要な重要問題です。
本書で扱う数的推理について例を挙げると、「割合」などの小学校の算数レベルの問題でも、定番の解き方をしっかりと理解しておくことが重要です。いざやってみると、意外とできなかったりするものです。信じがたい話かもしれませんが、割合を求めるはずなのに,まったく逆の計算をしてしまう受験生もいます。小学校の算数だからと高をくくらずに,「正しい知識」を「正しい勉強法」で「身につけておく」ことが、合格への第一歩なのです。
本書の到達目標として、「今後のアウトプットを効果的にするための正しい知識を使えるようになる」「有名な典型問題が解けるようになる」の2つが挙げられます。これらの目標に皆さんが達することができるように,最大限の工夫をしたつもりです。ぜひ、本書を使い倒して、試験に臨んでください。
最後に,皆さんの試験場でのご健闘および合格を心よりお祈り申し上げます。
2018年6月吉日
柴崎直孝
Contents
はじめに
目次
公務員採用試験の勉強法
第1章 数的推理の考え方
01 数的推理の考え方①
02 数的推理の考え方②
第2章 数の性質
03 倍数の性質①
04 倍数の性質②
05 掛け算に分解する問題
06 約数の個数
07 最大公約数と最小公倍数
08 最小公倍数と周期性
第3章 余りと不足
09 余りと不足(余り一致)
10 余りと不足(不足一致)
11 余りと不足(余り、不足ともに一致しない)
第4章 割合
12 割合
13 勝手に数値を設定できる問題の
14 勝手に数値を設定できる問題2
第5章 比
15 比の統一
16 比(割合を比に変換する)
17 比の性質①
18 比の性質②
19 比に文字を添えて実際の数値に見立て①
20 比に文字を添えて実際の数値に見立てる②
21 比例式
22 てんびん算
第6章 方程式
23 方程式
24 方程式と「勝手に数値設定」
25 平均算
26 仕事算と方程式
27 ニュートン算.
第7章 濃度
28 濃度の解法
(食塩の重さに着目して推理するタイプ)
29 濃度と方程式
30 濃度とてんびん
第8章 整数解
31 不定方程式の基本
32 不定方程式の裏技
第9章 速さ
33 速さと方程式(時間の等式)
34 速さと方程式(距離の等式)&ダイヤグラム
35 速さと比(時間が同じ場合)
36 速さと比(距離が同じ場合)
37 旅人算①
38 旅人算②
39 旅人算③
40 旅人算④
41 旅人算⑤
42 旅人算⑥
43 通過算
44 流水算
第10章 その他の文章題
45 変則仕事算
46 和の組合せ(偶数編)
47 和の組合せ(奇数編)
第11章 記数法
48 記数法の変換
49 記数法の応用
第12章 数列
50 等差数列①
51 等差数列②
52 階差数列
53 その他の規則性
第13章 覆面算・魔方陣
54 覆面算
55 魔方陣
第14章 場合の数
56 積の法則
57 和の法則
58 「隣り合う」といわれたら
59 樹形図
60 順列
61 組合せ①
62 組合せ②
63 分配問題(0個の人がいてもいい場合)
64 分配問題(少なくとも1個はもらう場合)
65 平行四辺形の個数
66 最短経路
第15章 確率
67 確率の定義①
68 確率の定義②
69 確率の定義③(じゃんけんの確率)
70 確率の足し算・掛け算
71 余事象の確率①
72 余事象の確率②
73 反復試行の確率
74 期待値
第16章 図形の計量
75 三平方の定理
76 有名な角度の直角三角形①
77 有名な角度の直角三角形②
78 相似比
79 相似比と面積比
80 相似比と体積比
81 底辺分割の定理
82 斜線部の面積
83 立体図形の計量の基礎(切断する場合)
84 立体図形の計量の基礎(展開する場合)
おわりに
索引
公務員採用試験の勉強法
ここでは、公務員試験(公務員採用試験)の流れと勉強法を説明します。本書で扱う数的推理だけでなく、公務員採用試験の全般について主に説明します。
公務員採用試験の大まかな流れ
公務員採用試験は「択一試験(マークシート試験)」、「論作文試験」,「面接試験」の3つに大別できます。皆さんが勉強を始めるにあたり、最初に着手するのは択一試験の対策となります。
公務員採用試験の大まかな流れ
択一試験について
公務員採用試験は、大学入試のような「少ない科目の、深い知識を問う試験」とは真逆の「多くの科目の,浅い知識を問う試験」です。教養,専門試験を合わせると30科目前後,教養試験のみの試験種でも約15科目が出題されます。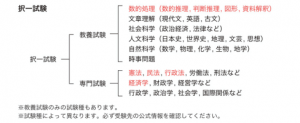
こんなにあると、どの科目から勉強していいのか迷ってしまいますね。まずは出題数が多い科目から始めましょう。教養試験の数的処理,専門試験の憲法,民法,行政法,経済学はどの試験でも多く出題されるので(公務員試験対策の予備校などでは「主要5科目」とよんでいます)まずはここから始めましょう。近年,教養試験のみの試験種も増えてきています。主要5科目のうち唯一の教養試験である数的処理の重要度が以前よりも増しています。
数的処理の特徴
教養試験はさらに、「知能分野」と「知識分野」に分かれます。数的処理は知能分野に属します。知能分野というだけあって知識だけではなく、発想力、読解力,情報処理能力といった頭の柔軟性が大事な試験です。その思考の仕方は独特で,慣れるまで時間がかかります(下図参照)。日本史や生物といった知識系の科目は基本的に暗記ですので、覚えれば覚えるほどその科目のレベルが上がります。しかし、数的処理は最初のうちは上達した実感が湧かないので、不安になってしまいます。下の図の★の、段々と上達が実感できるようになる時期まで、センスのある受験生でも3か月はかかるといわれています。数的処理が苦手な受験生は、6か月,9か月あるいは試験直前までまったく上達の実感が湧かないこともあります。
そういった受験生は一様に勉強の仕方がよくありません。次のページで正しい攻略法を解説します。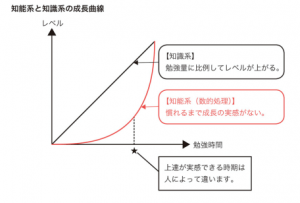
数的処理の攻略法~その1~
公務員採用試験は構造上、満点を取るのがほぼ不可能な試験です。試験によって異なりますが、教養試験は60%の正解率が合格ラインです。とはいえ数的処理で60%を取るのは結構大変です。
合格した受験生全員が数的処理で60%取れるようになっているのか?というとそうでもありません。多くの受験生が半分前後だけ正解し、文章理解と知識系で補っています。
まずは、「正答率50%程度=足を引っ張らないレベル」を目指しましょう。逆にいきなり60%を目指そうとする受験生は、最初から難問を解こうとするので「成長の実感」がいつまでたっても得られません。一歩一歩着実に進めていくイメージで勉強しましょう。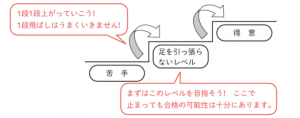
数的処理の攻略法~その2~
では、どうやったら足を引っ張らないレベルになれるのか? 数的処理は大きく分けると、「見たことあるパターン問題」と「非典型のひらめき問題」の2つがあります。どちらが解きやすいか?
当然前者です。パターン問題をマスターすることが50%取るための必要条件です。そこでまずはパターン問題の知識,公式,解法を覚えましょう。その役目を担ってくれるのが本書です。
知識を習得したらすぐに類題を解きましょう。漢字や英単語を10回書いて覚えたのと同じように、似た問題を集中して解くことで知識を焼きつけてください。
パターン問題の習得ができたら、「非典型のひらめき問題」を解きましょう。
この手の問題が解けるようになると数的処理は得点源になりますが、何度も述べている通り、解けるようにならなくても合格の可能性は十分にあります。
本書の構成
■重要度
パターンの出題頻度です。時間がない方は、Cランクは飛ばしてもいいです。
■到達目標
本書において最も大事なところです。当たり前ですが、掲載されている問題がそっくりそのまま本番の試験で出題されるのはレアです。皆さんが本書の問題を解くのは、同じパターンの問題を解くための知識を身につけるためです。では何を身につけるのか?何ができるようになればいいのか?
それが「到達目標」に記されています。ほぼすべての到達目標は「○○できるようになる」と書かれていますので,ゴールがイメージしやすいはずです。
■知識
皆さんに覚えてほしい公式,知識,解法を載せています。
問題によっては解説で紹介しています。
■出典
掲載した問題がどの試験で出題されたかを表示しておきます。しかし、本書の問題はどの試験でも出題される良問ばかりですので、出典にはこだわらず解いてください。なお国家公務員に関しては、制度変更前は「国家I種・国家II種・国税専門官・法務教官」,変更後は「国家総合職・国家一般職・国家専門職」と名称を変えて記載しています。
■難易度
数的処理が苦手な方は★1つ2つの問題から始めましょう。★3つは余裕ができてからでかまいません。★4つ以上はやや難問なので、やらなくてもかまいません。
数的推理について
数的推理は算数と数学の要素が含まれる問題が多数出題されます。民間の就職活動を経験した方なら「SPI(非言語分野)」を解いたことがあると思いますが、それに近いです(難易度は数的推理のほうが上です)。
したがって、算数と数学の基礎はある程度必須になります。とはいえすべてをやる必要はありません。以下に挙げるものはできるようにしておきましょう。
【数的推理を解きながらで覚えられるもの】
「最小公倍数・最大公約数の求め方」、「比・割合の計算」、「方程式の立て方」、「数列」、「記数法」、「場合の数・確率」、「三平方の定理」、「相似」
【数的推理を解く以前に知っていてほしい知識】
「分数の四則演算」,「方程式の途中計算」,「平方根」,「図形の面積」
関数や三角比などはめったに出題されないので、学習する必要はありません。冒頭でも書きましたが、数的推理は数学だけでなく算数の要素もあります(むしろ算数に近い)。
多くの受験生が勘違いしているところです(すべての文章題を方程式で解く悪癖がある)。まずは「約数・倍数」「比・割合」で算数の感覚を取り戻しましょう。第2章~第5章は軽視されがちですが、これらの章こそが数的 推理らしい問題の宝庫です。
速さに代表されますが、文章題を解くのに「方程式」と「比」を用います。私はこの2つを「道具」とよんでいます。数的推理の文章題はどちらの道具もバランスよく使える人が点を取れます。片一方に偏らないようにしましょう。
図形の計量はほぼすべての試験で1問は出題される人気分野です。
その半分が 「三平方の定理」と「相似」から出題されます。中学3年生の知識なので久しく忘れているかもしれませんが、有名な問題が多く出ますので、解いた問題は問題文を丸ごと覚える気持ちで習得しましょう。
次によく出題されるのが確率です。確率は計算以上に問題文を読解する力が求められます。公式に頼りすぎる人ほど苦手な傾向にあります。
数的推理は、計算が苦手な受験生にとっては苦痛に感じる分野です。まずは簡単な問題だけ解きましょう。他の科目で補えれば最悪の事態は免れるはずです。余裕ができたら徐々に難しい問題にもチャレンジしてみてください。一歩一歩、着実に行きましょう。
では健闘を祈ります。












