上・中級公務員標準数的推理―基礎から体系的に学べる“基本書”

はじめに
公務員試験の「数的推理」「判断推理」という科目を大学セミナーや種々の講習会で教えるようになって15年を超えた。講義で使用したプリント類の量 は、手元に残っているものだけでもかなりのものになる。これらをまとめたものが、本書の『標準 数的推理』であり、『標準 判断推理』であった。これ らの2冊に共通していえることは、体系的にまとめられ,応用範囲の広い考 え方を身につけることができるように書かれたものということである。「準備の段階で、過去の出題を調べ,分類するところから始めた。基本的な 概念を詳しく説明し、代表的な問題や応用範囲の広い問題を例題として解説し、少しずつ難易度の高い問題へ移るように配慮してある。枝葉末節と思われる問題はできる限り外し、思考力を伸ばすような問題を多く載せた。また今回の改訂にあたっては、例題や練習問題を大幅に増やした。

読者はまず、【基本事項】をじっくりと読み、用語や約束事、解答に至る考え方を身につけてほしい。【例題】は、読むだけでなく何度でも鉛筆を持って 実際に解答を追いかけてみるとよい。そして納得のいったところで【練習問 題]に進み、自分の理解したことを試してほしい。
「数的推理」は、「判断推理」と比較して,数学との類似性が高い分、読者 の読み方も多様になるであろう。文科系の学生諸君や、数学としばらく縁の なかった人たちは、何度も繰り返し【基本事項】や【例題】を読み、必ず鉛筆を手にして一つ一つ確認して進んでいくことをお勧めする。また,第4章 の剰余類の考え方は慣れるまでに時間がかかるので、後回しにして先に進んでもよい。
先の『標準 判断推理』がそうであったように、この『標準 数的推理』を 出版する目的の一つは、学生諸君がこれらの科目を学ぶときの「標準」的な道筋を指し示すことにある。本書および『標準 判断推理』がそうした要求を満たすものとなることを願っている。
2001年7月
田辺勉
目次
第1章 方程式
基本事項1 文字少使用,連立方程式解法
基本事項2 時計算
基本事項3 2次方程式
練習問題 練習問題の解説
第2章 不等式
基本事項1 不等式 基本事項22次不等式
練習問題 練習問題の解説
第3章 整数その1(倍数・約数)
基本事項1倍数・約数、倍数の見分け方
基本事項2 最大公約数・最小公倍数
練習問題
練習問題の解説
第4章 整数 02(剩余類)
基本事項1 剩余類 基本事項2 剩余類D演算
練習問題
練習問題の解説
第5章 整数 03(虫くい算·覆面算·魔方陣)
基本事項1 虫くい算、覆面算
基本事項2 魔方陣
練習問題 練習問題の解説
第6章 整数 その4 (n進法)
基本事項1 n進法
基本事項2 10進法の数をn進法に直す
基本事項3 n進法の数をm進方に直す
練習問題 練習問題の解説
第7章比・割合
基本事項1 比·割合
基本事項2 濃度
基本事項3仕事算
練習問題 練習問題の解説
第8章 速含·距離・時間
基本事項1 速さ・距離・時間
基本事項2 流水算
基本事項3 通過算
練習問題
練習問題の解説
第9章 座標・グラフ・数列
基本事項1 座標・グラフ
基本事項2ダイアグラム
基本事項3 数列
練習問題 練習問題の解説
第10章 平面図形その1
基本事項1 平行線
基本事項2 平行線と線分の比
基本事項3平面図形の面積
基本事項 4 線分比と面積比
練習問題の解説
第11章 平面図形その2(三平方の定理)
基本事項1三平方の定理
基本事項2 重心・外心・内心.
練習問題の解説
第12章平面図形その3(円)
基本事項1円周角の定理
基本事項2 接弦定理
基本事項3方べきの定理
練習問題
練習問題の解説
第13章 空間図形
基本事項1 基本的な空間図形
基本事項2体積・表面積
基本事項3面上の2点間の最短距離
練習問題
練習問題の解説
第14章 場合の数
基本事項1 場合の数
基本事項2 順列
基本事項3 組合せ
基本事項4 重複組合せ
練習問題 練習問題解説
第15章確率
基本事項1 確率
基本事項2 和事象·積事象
基本事項3独立試行の確率
練習問題
練習問題の解説
索引
第1章 方程式
周囲の空無を生み出し、しかもその空無を必要とする 白い光の球として星を見る、全く新しい奇妙な知覚。 ひいては、その知覚と関連して,私も全く同じように 暗黒の空無の中に吊り下げられているという感覚。私は星を見つめ、星は私を見つめていた。私と星との間 には釣り合いが保たれ、もしも意識を重量で現すことができるとすれば、正確に等しい二つの重さが天秤の水平状態を維持していた。
シージョン・ファウルズ『魔術師」
解說
この章では文字を使って、方程式を立てて解く問題を解説する。いわゆる文章題で、年齢算、時計算,過不足算のようなものも方程式でやさしく解いてみることにする。また2次方程式についても簡単に触れることにする。
基本事項1 文字の使用・連立方程式の解法
文字を使って数量を表したり、方程式を立てたりすることができる。以下の文音 から文字を用いて式を作ってみよう。
1辺がacmの正方形の周の長さは,4a(cm)
時速xkmでv 時間走ったときの距離 km は, z=xy と表せる。
十の位がx,一の位がりである整数は, 10x+y
120gのx%は,120× x /100=6 /5x(g)
半径rの球の表面積は47、体積は4/3πr
ここではまず、いくつかの代表的な2元連立1次方程式の解き方を具体例で示し、 方程式の解法の基本を習得してもらう。代入法や加減法などがあげられているが, いずれの場合も文字を減らしていき、よりやさしい方程式や、簡単な場合に還元し ていく。また、解が出たら面倒がらずにできる限り検算をする癖をつけてほしい。

②x=11 y=14
③x=5 y=ー1 /2
◆文章題への応用 文章題を方程式で解くには,普通,以下のような手順で行う。 文章で与えられた問題を熟読し、わかりにくけれは図や衣を使って意味をよく理 解し、与えられたものが何で,求めるものは何かをはっきりさせる。求めるもの。 あるいはそれに関連のある未知の数値を文字で表す。問題の数量関係を式で表す。 それを解いて、最終的に問題の要求している数値を出す。その解が問題に適してい
るかを確かめる。
過不足算,鶴亀算と呼ばれるなつかしい例でその様子を見てみよう。
(例)鉛筆を何人かの生徒に分けるのに、1人6本ずつ分けると2本不足し、1人5本ずつ分けると15本余る。生徒の人数と鉛筆の本数を求めよ。 (考え方) 求めるものは生徒の人数と鉛筆の本数の2つだが,文字(未知数)は少ないほうが楽なので、1つですめばそれにこしたことはない。生徒の 人数xがわかれば、鉛筆の本数は6x-2ですぐに求められるので1つだけにする。 (解) 生徒の人数をxとする。
「1人6本ずつ分けると2本不足する」ことから,鉛筆の本数は(6x-2)本 と表され、また,「1人5本ずつ分けると15本余る」ことから,(5x+15)本と も表される。したがって,この2つの式から次の方程式が得られる。
6x-2=5x+15 1 x=17
鉛筆の本数は、6x-2または5x+15にx=17を代入して求める。
6×17-2-31001
答生徒の人数17人 鉛筆の本数100本 (2) いかとたこ合わせて20匹いる。その足の数は、いかとたこを合わせて174本ある。いかとたこはそれぞれ何匹いるか。 (解) いかを匹,たこを匹と置く。
合わせて20匹だから x+y=320 足の本数を考えて10x+8y%3D174 これを解いて、
x=7,v=13 答いか たこ 135
【例題1-1】
父,母と子供が1人いる。母は父より4歳若く、父と母の年齢の和は子供の年齢の5倍に等しい。6年前には母の年齢が子供の年齢の3倍であったという。父と母の年齢の和が子供の年齢の4倍になるのは何年後か。
1 6年後
2 7年後
3 8年後
4 9年後
5 10年後
【例題1-1の解説】
基本事項2 時計算
時計の長針と短針が特別な位置関係になる時刻を問う問題。長針と短針が重なっ たり、一直線上に並んだり、直角になったりする時刻を求める。
12時の位置から時計回りに何度動いた位置に針があるかで考えるとよい。長針と 短針では一定の時間に動く角度に違いがあるので,単位時間あたりの動く量を求めておく。
1時と2時の間で長針と短針が重なるのは1時何分か。 (解)重なる時刻を1時x分とする。 「そのときの長針の位置は、0時(12時)から6x°のところ。 また、短針の位置は,0時から30~+0.5x°のところ。 長針と短針が重なるから。
6x=30+0.5x 両辺を2倍して、まとめると
11x=60
x=11/60=5+5/11
5 /11分は300/11秒=27+3/11秒
よって、求める時刻は約1時5分27秒
時計算
12時の位置から何度のところにあるか。
長針…1分あたり 6°
短針…1時間当たり 30°
1分あたり 0.5°
例題1−2
8時から1時間の間に、時計の長針と短針は1度だけ正反対の位置に一直線上に並ぶ。それは何時何分か。
1 8時9 1 /11分
2 8時10 9 /11分
3 8時10 10/11分
4 8時11 1/11分
5 8時11 11/9分
(例題1−2の解説)
求める時刻を8時x分とする。
長針の位置は、6x°
短針の位置は、8×30 +0.5x 長針の位置の180°反対側が短針の位置だから,
6x +180=240 +0.5x
両辺を2倍してまとめると、11x=120
x=11/120=10+11/10
よって、求める時刻は8時10 11/10分
基本事項 3 2次方程式
●因数分解
2次方程式の解法 (1)
解の公式
2次方程式の解法⑵

解と係数の関係
例題1−4
1辺が1cmの小立方体を組み合わせて立方体 A を作ると小立方体がx 個残る。 残った小立方体を立方体Aの表面に付着させてひと回り大きい(1辺の長さが1 cm 長い)立方体Bを作ると、今度は小立方体が75個残る。しかし,立方体B より さらにひと回り大きい立方体Cを作ろうとすると,小立方体が142個足りなくなる という。xはいくらか。
1 243
2 244
3 245
4 246
5 247
【例題1-4の解説】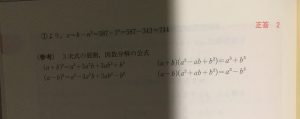
練習問題
No.1
ある試験で受験者の4割の人が合格したという。受験者全員の平均点は60 点で、合格者の平均点は合格最低点より15点高く,不合格者の平均点は合格最低 点より20点低かったという。合格最低点は何点か。
1 69点
2 68点
3 67点
4 66点
5 65点
No.2
A, B,C,Dの4人である品物を買った。 A は全体の代金の半分を, B は他の3人の出したお金の1/3を、Cは他の3人の出したお金の1/4を,Dは残りの 5500円を払った。この品物の代金はいくらか。
1 25000円
2 20000円
3 15000円
4 10000円
5 5000円
No.3
現在の父の年齢は子供の2.5倍である。8年後には、父の年齢が子供の年齢の2倍になるという。現在の父の年齢はいくつか。
1 30歳
2 35歳
3 40歳
4 45歳
5 50歳
No.4
みかん何個かを1人につき5個ずつ配ると10個余り、この人数の3倍より 5人少ない人数に、1人につき2個ずつ配ると8個不足する。このみかんを1人 につき6個ずつ配ると、何人に配ることができるか。
1 21人
2 22人
3 23人
4 24人
5 25人
No.5
午後6時から1時間の間に時計の長針と短針は1度だけ重なる。それは何時何分か。
1 午後6時32 6/11分
2 午後6時32 7/11 分
3 午後6時32分 8/11分
4 午後6時32分 9/11分
5 午後6時32分 10/11分
No. 6
現在2時で長針と短針のなす角度は60°である。長針と短針のなす角度が再び60°になるのは何分何秒後か。
1 20分27秒後
2 20分41秒後
3 21分16秒後
4 21分49秒後
5 22分10秒後
No. 7
A, B, C, D, Eの5人の月収の合計額は,130万円である。AとBの合計額は62万円、AとCの合計額は56万円,A とDの合計額は45万円, DとEのム 額は37万円である。Eの月収はいくらか。
1 12万円
2 14万円
3 17万円
4 20万円
5 22万円
No. 8
A, B2種類の茶があり,100gあたりの単価は A のほうがBより50円高い。また, A を100円分買ったときの量は、Bを100円分買ったときの量より10g 少ない。では、A, Bを合わせて600g買い、しかもAの量がBの量の2倍になるようにすると、購入金額はいくらになるか。
1 1250円
2 1300円
3 1350円
4 1400円
5 1450円
No. 9
No. 10
No. 11
両親と長女,次女の4人家族がいる。現在の両親の年齢の和は、2人の子供の年齢の和の5倍であるが、2年後には4倍になるという。また,現在の母親の年齢は、次女の7倍で,父親より4歳下であるという。長女と次女の年齢 いくらか。
1 2歳
2 3歳
3 4歳
4 5歳
5 6歳
No. 12
練習問題の解説
No. 1
受験者数を4人とすると、合格者数は0.4a 人,不合格者数は0.6a 人。受験 者の平均点が60点であるから、受験者の総得点は604点となる。求める合格最低点を差点とすると、合格者の平均点はx+15点,不合格者の平均点はx-20点。合格者の総得点は0.4a(x+15) 点,不合格者の総得点は0.6a(x-20) 点であるから、
60a=0.4a(x+15)+0.6a(x-20)
という方程式が得られる。
両辺に10をかけ、aで割ると、
600=4x+60+6x-120
10x=660
x=66
No.2
求める品物の代金をx円とする。また、B、Cの出した金額をそれぞれ b円、c円とすると,B,Cはそれぞれ、他の3人が出した金額の1/3、1/4を払ったから、
b=1/3(xーb) b=x /4
c=1/4(x -c) c=x /5
Aはx /2円払い、A、B、C、D4人の合計金額がxになるから、
x /2+x /4+x /5+500=x
両辺に20をかけて、分母を払うと、10x+5x+4x+10000=20x
x= 10000(円)
No. 3
現在の子供の年齢をxとすると,現在の父親の年齢は2.5x。8年後 年齢が子供の年齢の2倍になるから,
2.5x+8=2(x+8) . x=16
現在の父親の年齢は2.5x だから、2.5x=40
No.4
最初の人数をx人とする。みかんの個数は5x+10個。
この人数の3倍より5人少ない人数に、1人につき2個ずつ配ると8個不足するから。
5x+10=2(3x-5)-8
これを解いて、x=28
したがって、みかんの個数は150個。これを1人につき6個ずつ配ると,
150÷6=25
より、25人に配ることができる。
No.5
No.6
No.7
A, B,C,D,Eの5人のそれぞれの月収を a, b, c, d, e (万円)とす ると、
a+b+c+d+e=130…①
a+b=62 …②
a+c=56 …③
a+d=45…④
d+e=37 …⑤
②+⑤より a+b+d+e=99
①から引くと, c=31
③から、 a=25
④から、d=20
⑤から、e=17
よって、Eの月収は17万円。
No.8
No.9
No.10
解と係数の関係より,
a+β=4/3、aβ=-11/3
1/a-1+1/β-1=β-1+a-1/(a-1)(β-1)=a=β-2/aβ-(a+β)+1
=4/3-2/-11/3-4/3+1=4-6/-11-4+3=-2/-12=1/6
No.11
現在の次女の年齢をx歳とすると、母親は7x歳,父親は(7x+4)歳上
る。現在の長女の年歳をy歳とする。 現在の両親の年齢の和は、2人の子供の年齢の和の5倍であるから.
5(x+y)=327x+7x+4…….①
また、2年後に4倍になるから,
4{(x+2)+(y+2)}=7x+2+7x+6……. ②
②より, 14x=4(x+y)+8
これを①に代入して 5(x+y)=4(x+y)+8+4
x+y=12
これと①より, x=4, y=8
長女が8歳,次女が4歳なので、2人の年歳差は4歳。
No.12
Aの答は②を,Bの答は①を満たすはずだから、代入してみる。
61/26×8+27/13b=25 b=3
8/5a-61/5=-1 a-7
したがって,もとの方程式は
(7x+5y=-1
(8x-3y=25
これを解くと,(x,y)=(2,-3)
よって,x+y=2+(-3)=-1




